
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
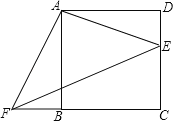
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
【答案】(1)见解析;(2)A、90;(3)50(平方单位)
【解析】
试题分析:(1)根据正方形的性质得AD=AB,∠D=∠ABC=90°,然后利用“SAS”易证得△ADE≌△ABF;
(2)由于△ADE≌△ABF得∠BAF=∠DAE,则∠BAF+∠BAE=90°,即∠FAE=90°,根据旋转的定义可得到△ABF可以由△ADE绕旋转中心 A点,按顺时针方向旋转90 度得到;
(3)先利用勾股定理可计算出AE=10,再根据△ABF可以由△ADE绕旋转中心 A点,按顺时针方向旋转90 度得到AE=AF,∠EAF=90°,然后根据直角三角形的面积公式计算即可.
(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=90°,
而F是CB的延长线上的点,
∴∠ABF=90°,
在△ADE和△ABF中
 ,
,
∴△ADE≌△ABF(SAS);
(2)解:∵△ADE≌△ABF,
∴∠BAF=∠DAE,
而∠DAE+∠EAB=90°,
∴∠BAF+∠EAB=90°,即∠FAE=90°,
∴△ABF可以由△ADE绕旋转中心 A点,按顺时针方向旋转90 度得到;
故答案为A、90;
(3)解:∵BC=8,
∴AD=8,
在Rt△ADE中,DE=6,AD=8,
∴AE=![]() =10,
=10,
∵△ABF可以由△ADE绕旋转中心 A点,按顺时针方向旋转90 度得到,
∴AE=AF,∠EAF=90°,
∴△AEF的面积=![]() AE2=
AE2=![]() ×100=50(平方单位).
×100=50(平方单位).


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是( )
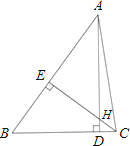
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AC∥BD,连接AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)
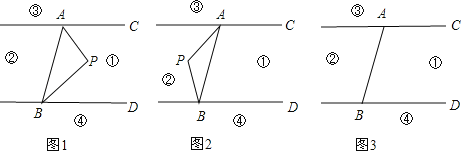
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
(3)当动点P落在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )

A. 2 B. 3 C. 1 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( ).
A.a3+a2=a5
B.a6÷a2=a3
C.(﹣3a2)2a3=﹣6a6
D.(﹣ab﹣1)2=a2b2+2ab+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A、C分别在x轴、y轴的正半轴,抛物线y=﹣![]() x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
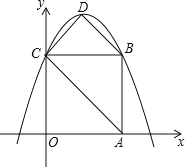
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB=CD,AD=BC,且![]() ,点P、Q分别是边AD、AB上的动点.
,点P、Q分别是边AD、AB上的动点.
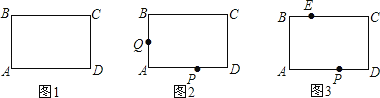
(1)求BD的长;
(2)①如图2,在P、Q运动中是否能使△CPQ成为等腰直角三角形?若能,请求出PA的长;若不能,请说明理由;
②如图3,在BC上取一点E,使EC=5,那么当△EPC为等腰三角形时,求出PA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com