
【题目】如图1,长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB=CD,AD=BC,且![]() ,点P、Q分别是边AD、AB上的动点.
,点P、Q分别是边AD、AB上的动点.
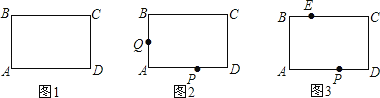
(1)求BD的长;
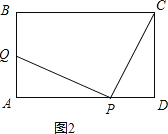
(2)①如图2,在P、Q运动中是否能使△CPQ成为等腰直角三角形?若能,请求出PA的长;若不能,请说明理由;
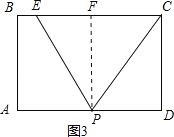
②如图3,在BC上取一点E,使EC=5,那么当△EPC为等腰三角形时,求出PA的长.
【答案】(1)![]() (2)①能,AP=4,理由见解析②3、3.5或4.
(2)①能,AP=4,理由见解析②3、3.5或4.
【解析】
试题分析:(1)由条件可求得AB=4,BC=6,由勾股定理可求出BD的长;
(2)①由题可知只能有∠QPC为直角,当PQ=PC时,可证得Rt△PDC≌Rt△QAP,可求得AP的长;②分PC=EC、PC=PE和PE=EC三种情况分别利用等腰三角形的性质和勾股定理求解即可.
解:
(1)如图1,连接BD,

∵![]() ,
,
∴AB=4,BC=6,
则在Rt△ABD中,由勾股定理可求得BD=![]() =2
=2![]() ;
;
(2)①能,AP=4,理由如下:
如图2,由图形可知∠PQC和∠PCQ不可能为直角,所以只有∠QPC=90°,则∠QPA+∠CPD=∠PCD+∠CPD,
∴∠QPA=∠PCD,
当PQ=PC时,
在Rt△APQ和Rt△DCP中
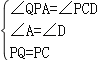
∴△APQ≌△DCP(AAS),
∴AP=CD=4,
故在P、Q运动中是否能使△CPQ成为等腰直角三角形,此时AP=4;
②当PC=EC=5时,在Rt△PCD中,CD=4,PC=EC=5,由勾股定理可求得PD=3,所以AP=AB﹣PD=3,
当PC=PE=5时,如图3,过P作PF⊥BC交BC于点F,则FC=EF=PD=![]() EC=2.5,所以AP=AB﹣PD=6﹣2.5=3.5,
EC=2.5,所以AP=AB﹣PD=6﹣2.5=3.5,
当PE=EC=5时,如图4,过E作EH⊥AD于点H,由可知AH=BE=1,在Rt△EHD中,EH=AB=4,EP=5,由勾股定理可得HP=3,所以AP=AH+PH=1+3=4,
综上可知当△EPC为等腰三角形时,求出PA的长为3、3.5或4.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
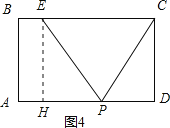
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5μm(1μm=0.000001m)的颗粒物,也称为可入肺颗粒物,它们含有大量的有毒、有害物质,对人体健康和大气环境质量有很大危害.2.5μm用科学记数法可表示为( )
A.2.5×10﹣5m B.0.25×10﹣7m C.2.5×10﹣6m D.25×10﹣5m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】指出下列命题的条件和结论.
(1)两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
(2)如果∠1=∠2,∠2=∠3,那么∠1=∠3.
(3)锐角小于它的余角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=kx2﹣2kx﹣3k交x轴于A、B两点,交y轴于点C,已知OC=OB.
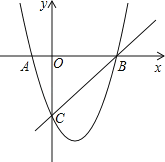
(1)求抛物线解析式;
(2)在直线BC上求点P,使PA+PO的值最小;
(3)抛物线上是否存在点Q,使△QBC的面积等于6?若存在,请求出Q的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】环境空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为( ).
A.2.5×10﹣5 B.2.5×105 C.2.5×10﹣6 D.2.5×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当多边形的边数每增加1时,它的内角和与外角和( )
A. 都增加180°
B. 都不变
C. 内角和增加180°,外角和不变
D. 内角和增加180°,外角和减少180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com