
【题目】如图,抛物线y=kx2﹣2kx﹣3k交x轴于A、B两点,交y轴于点C,已知OC=OB.
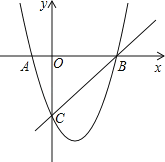
(1)求抛物线解析式;
(2)在直线BC上求点P,使PA+PO的值最小;
(3)抛物线上是否存在点Q,使△QBC的面积等于6?若存在,请求出Q的坐标;若不存在请说明理由.
【答案】(1)y=x2﹣2x﹣3,(2)(![]() ,﹣
,﹣![]() ),(3)存在点Q(﹣1,0)或(4,5),使△QBC面积等于6.
),(3)存在点Q(﹣1,0)或(4,5),使△QBC面积等于6.
【解析】
试题分析:(1)令y=0可得A,B的坐标,令x=0求出点C的坐标,再根据OC=OB求出k即可得抛物线解析式;
(2)作O的关于BC的对称点O′,连接AO′与BC交于点P,此时PA+PO的值最小,先求出AO′所在的直线与BC所在直线联立可求出交点P的坐标.
(3)在y轴上取一点E(0,1),过点E作ED⊥BC于点D,则△CBE的面积等于6,过点E作EQ平行于BC,交抛物线于点Q,运用直线EQ的解析式与抛物线联立求出点Q的坐标,注意BC下面的另一条与抛物线组成的方程无实根,没有交点.
解:(1)∵抛物线y=kx2﹣2kx﹣3k,
令y=0得0=kx2﹣2kx﹣3k,即0=x2﹣2x﹣3,
解得x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0)
令x=0得y=﹣3k,
∴点C(0,﹣3k),
∵OC=OB,
∴3k=3,解得k=1,
∴抛物线解析式为:y=x2﹣2x﹣3,
(2)如图1,作O的关于BC的对称点O′,连接O′C,O′B,连接AO′与BC交于点P,此时PA+PO的值最小
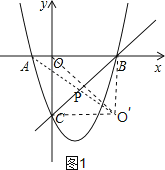
∵OC=OB,OO′⊥BC,
∴BC被OO′平分,
∴四边形OBO′C是正方形,
∴点O′的坐标为(3,﹣3),
∵A(﹣1,0),设AO′所在的直线的解析式为y=kx+b,
∴![]() ,解得
,解得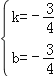 ,
,
∴AO′所在的直线的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
由B(3,0),C(0,﹣3)得BC所在直线的解析式为y=x﹣3.
∴联立组成方程组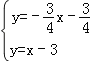 ,解得
,解得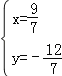 ,
,
∴直线AO′与直线BC的交点P的坐标为(![]() ,﹣
,﹣![]() ),
),
(3)存在
如图2,
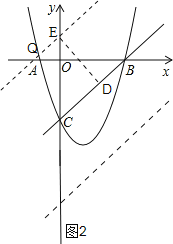
∵△QBC的面积等于6,
∴△QBC的面积=![]() BCh,
BCh,
∵OC=OB=3
∴BC=3![]() ,
,
∴h=6×2÷3![]() =2
=2![]() .
.
∵∠OCB=45°,
∴在y轴上取一点E(0,1),过点E作ED⊥BC于点D,则△CBE的面积等于6,过点E作 EQ平行于BC的平行线y=x+1,交抛物线于点Q,
由![]() ,解得
,解得![]() 或
或![]() ,
,
∴Q(﹣1,0)或(4,5)
同理当E点的坐标为0,﹣7)时直线解析式为:y=x﹣7,
由![]() ,得x2﹣3x+4=0,△<0,方程无实根.
,得x2﹣3x+4=0,△<0,方程无实根.
综上存在点Q(﹣1,0)或(4,5),使△QBC面积等于6.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】定义两种新变换:①f(a,b)=(a,-b),如f(1,2)=(1,-2);②g(a,b)=(b,a),如g(1,2)=(2,1).据此得g(f(5,-6))=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB=CD,AD=BC,且![]() ,点P、Q分别是边AD、AB上的动点.
,点P、Q分别是边AD、AB上的动点.
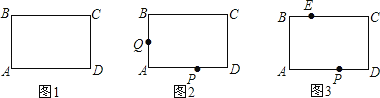
(1)求BD的长;
(2)①如图2,在P、Q运动中是否能使△CPQ成为等腰直角三角形?若能,请求出PA的长;若不能,请说明理由;
②如图3,在BC上取一点E,使EC=5,那么当△EPC为等腰三角形时,求出PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若某地打长途电话3分钟之内收费1.8元,3分钟以后每增加1分钟(不到1分钟按1分钟计算)加收0.5元,当通话时间t≥3分钟时,电话费y(元)与通话时间t(分)之间的关系式为___________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠1与∠2是两条直线被第三条直线所截的同位角,若∠1=50°,则∠2为( )
A. 50° B. 130° C. 50°或130° D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论正确的是( )
A. 有两个锐角相等的两个直角三角形全等; B. 一条斜边对应相等的两个直角三角形全等;
C. 顶角和底边对应相等的两个等腰三角形全等; D. 两个等边三角形全等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com