
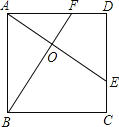
【题目】如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有( )
A.1个 B.2个 C.3个 D.4个
【答案】A
【解析】
试题分析:根据四边形ABCD是正方形及CE=DF,可证出△ADE≌△BAF,则得到:①AE=BF,以及△ADE和△BAF的面积相等,得到;④S△AOB=S四边形DEOF;可以证出∠ABO+∠BAO=90°,则②AE⊥BF一定成立.错误的结论是:③AO=OE.
解:∵四边形ABCD是正方形,
∴CD=AD
∵CE=DF
∴DE=AF
∴△ADE≌△BAF
∴AE=BF(故①正确),S△ADE=S△BAF,∠DEA=∠AFB,∠EAD=∠FBA
∵S△AOB=S△BAF﹣S△AOF,
S四边形DEOF=S△ADE﹣S△AOF,
∴S△AOB=S四边形DEOF(故④正确),
∵∠ABF+∠AFB=∠DAE+∠DEA=90°
∴∠AFB+∠EAF=90°
∴AE⊥BF一定成立(故②正确).
假设AO=OE,
∵AE⊥BF(已证),
∴AB=BE(线段垂直平分线上的点到线段两端点的距离相等),
∵在Rt△BCE中,BE>BC,
∴AB>BC,这与正方形的边长AB=BC相矛盾,
∴,假设不成立,AO≠OE(故③错误);
故错误的只有一个.
故选:A.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
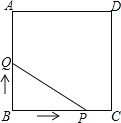
A.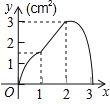 B.
B.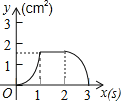
C.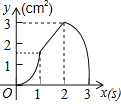 D.
D.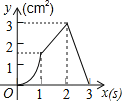
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AC∥BD,连接AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)
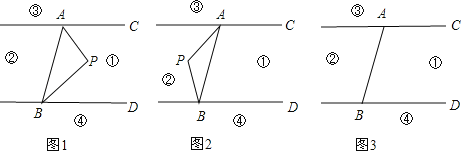
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
(3)当动点P落在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )

A. 2 B. 3 C. 1 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( ).
A.a3+a2=a5
B.a6÷a2=a3
C.(﹣3a2)2a3=﹣6a6
D.(﹣ab﹣1)2=a2b2+2ab+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元时,则每个月少买5件(每件售价不能高于65元),设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大利润是多少?
(3)每件商品的售价定为多少元时,每个月的利润恰为3200元?根据以上结论,请你直接写出售价在什么范围内,每个月的利润不低于3200元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com