
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��40Ԫ���ۼ�Ϊÿ��50Ԫ��ÿ���¿�����210�������ÿ����Ʒ���ۼ�ÿ����1Ԫʱ����ÿ��������5����ÿ���ۼ۲��ܸ���65Ԫ������ÿ����Ʒ���ۼ�����xԪ��xΪ����������ÿ���µ���������ΪyԪ��
��1����y��x�ĺ�����ϵʽ��ֱ��д���Ա���x��ȡֵ��Χ��
��2��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���¿ɻ�����������������Ƕ��٣�
��3��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���µ�����ǡΪ3200Ԫ���������Ͻ��ۣ�����ֱ��д���ۼ���ʲô��Χ�ڣ�ÿ���µ�������3200Ԫ��
���𰸡���1��y=��5x2+160x+2100��0��x��15��xΪ����������2�����ۼ۶�Ϊÿ��65Ԫ��ÿ���µ��������������������3375Ԫ����3���ۼ��ڲ�����60�Ҳ�����65Ԫ֮��ʱ��ÿ���µ�������3200Ԫ��
��������
�����������1������������������Ǽ۸�Ĺ�ϵʽ��Ȼ���ٸ�����������=������ÿ���������г���ϵʽ��
��2������������ߵĶԳ��ᣬȻ�����ݶ��κ���������ȷ�����������ʹ�ʱ���ۼۣ�
��3����y=3200���õ�����x��һԪ���η��̣�Ȼ����x��ֵ���ɣ�Ȼ����ݶ��κ��������ʿ�����Ա����ķ�Χ��
�⣺��1��������ã�y=��210��5x����50+x��40��
=��5x2+160x+2100��0��x��15��x��������
��2����x=��![]() =��
=��![]() =16��
=16��
�������ߵĶԳ���Ϊx=16��
��a=��5��0��
����0��x��15ʱ��y��x�����������
����x=15ʱ��ÿ���µĻ���������ֵΪ3375Ԫ��
50+15=65Ԫ��
�����ۼ۶�Ϊÿ��65Ԫ��ÿ���µ��������������������3375Ԫ��
��3����y=3200ʱ����5x2+160x+2100=3200��
��ã�x1=10��x2=22����ȥ����
����x=10ʱ��������=50+10=60Ԫ��
�����ۼ۶�Ϊÿ��60Ԫʱ��ÿ���µ�����Ϊ3200Ԫ��
���ۼ��ڲ�����60�Ҳ�����65Ԫ֮��ʱ��ÿ���µ�������3200Ԫ��


 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��E��F�ֱ���������ABCD�ı�CD��AD�ϵĵ㣬��CE=DF��AE��BF�ཻ�ڵ�O�����н��ۢ�AE=BF����AE��BF����AO=OE����S��AOB=S�ı���DEOF�У�������У� ��
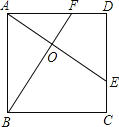
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������OΪԭ���ƽ��ֱ������ϵ�У���֪��A��3��2���͵�B��3��4��������OAB�����Ϊ��������
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������˶�����ƽ�Ƶ��ǣ� ��
A. ����ʱ��ҳ B. �����������˶�
C. ʿ�����ӿ������ת D. ������·��ת��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��PM2.5��ָ������ֱ��С�ڻ����2.5��m��1��m=0.000001m���Ŀ����Ҳ��Ϊ����ο�������Ǻ��д������ж����к����ʣ������彡���ʹ������������кܴ�Σ����2.5��m�ÿ�ѧ�������ɱ�ʾΪ�� ��
A��2.5��10��5m B��0.25��10��7m C��2.5��10��6m D��25��10��5m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ָ����������������ͽ�����
(1)����ֱ�߱�������ֱ�����������ͬ���ڽǻ�������ô������ֱ��ƽ����
(2)�����1����2����2����3����ô��1����3.
(3)��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ŶԱ�ƽ�е�ֽ�������⽻�������һ��ת�����е�һ�ţ��غϵIJ��ֹ�����һ���ı��Σ�����ı����� ��
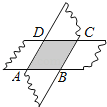
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com