
【题目】为了了解全校3000名学生对学校设置的体操、球类、跑步、踢毽子等课外体育活动项目的喜爱情况,在全校范围内随机抽取了若干名学生.对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的条形统计图和扇形统计图(均不完整).
(1)在这次问卷调查中,一共抽查了多少名学生?
(2)补全条形统计图;
(3)求“球类”所对应的扇形的圆心角度数;
(4)估计该校3000名学生中有多少人最喜爱球类活动?
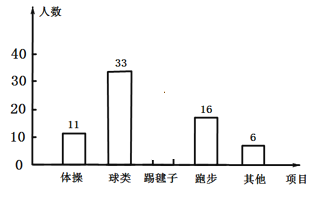
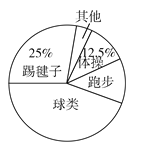
【答案】(1) 88人;(2) 见解析;(3) ![]() ;(4) 1125人
;(4) 1125人
【解析】
(1)利用体操的频数和百分比即可求得答案;
(2)利用总数和踢毽子的百分比可求出其频数,补全图象即可;
(3)根据“球类”的人数即可得出扇形圆心角的度数;
(4)根据样本估计总体,即可得出估计全校最喜欢球类活动的人数.
(1)根据条形统计图知参加体操的人数为11人,占扇形图的12.5%,
∴11÷12.5%=88(人),
∴一共抽查了88人;
(2)踢毽子的人数=88×25%=22(人),
补全条形统计图如图所示:
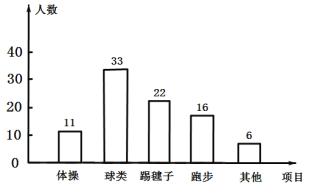
(3)扇形统计图中表示“球类”项目扇形圆心角的度数为![]() ;
;
(4)3000×![]() (人).
(人).
估计全校有1125人最喜欢球类活动.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】上海首条中运量公交线路71路已正式开通.该线路西起沪青平公路申昆路,东至延安东路中山东一路,全长17.5千米.71路车行驶于专设的公交车道,又配以专用的公交信号灯.经测试,早晚高峰时段71路车在专用车道内行驶的平均速度比在非专用车道每小时快6千米,因此单程可节省时间22.5分钟.求早晚高峰时段71路车在专用车道内行驶的平均车速.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O按顺时针方向旋转120°得到△OA′B′,则点A′的坐标是( ) 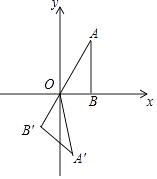
A.(2,﹣2 ![]() )
)
B.(2,﹣2 ![]() )
)
C.(2 ![]() ,2)
,2)
D.(2 ![]() ,2)
,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(甲车休息前后的速度相同),甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示.根据图象的信息有如下四个说法:①甲车行驶40千米开始休息②乙车行驶3.5小时与甲车相遇③甲车比乙车晚2.5小时到到B地④两车相距50km时乙车行驶了![]() 小时,其中正确的说法有( )
小时,其中正确的说法有( )
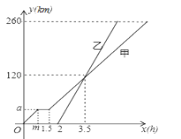
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、F、C、E在一条直线上,AC=DF,BF=CE,那么添加下列一个条件后,仍无法判断△ABC≌△DEF的是( )
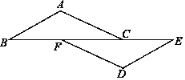
A. ∠A=∠D=90° B. ∠BCA=∠EFD C. ∠B=∠E D. AB=DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com