
分析 (1)设m2+m+4=k2(k为非负整数),则有m2+m+4-k2=0,由m为整数知其△为完全平方数,即1-4(4-k2)=p2(p为非负整数),(2k+p)(2k-p)=15,显然2k+p>2k-p,再分别求出a、b、c的值即可;
(2)根据题意易得($\frac{m+n}{\sqrt{2}}$)2+($\frac{m-n}{\sqrt{2}}$)2+p2=m2+n2+p2,又由32+(-4)2+(-1)2≠2012,即可证得结论.
解答 解:(1)设m2+m+4=k2(k为非负整数),则有m2+m+4-k2=0,
由m为整数知其△为完全平方数,即1-4(4-k2)=p2(p为非负整数),(2k+p)(2k-p)=15,显然2k+p>2k-p,
∴$\left\{\begin{array}{l}{2k+p=15}\\{2k-p=1}\end{array}\right.$或$\left\{\begin{array}{l}{2k+p=5}\\{2kp=3}\end{array}\right.$,
解得:p=7或p=1,
∴m=$\frac{-1±p}{2}$,
∴m1=3,m2=-4,m3=0,m4=-1,
∴a=3,b=-4,c=-1.
(2)三个数,任意两个求其和,再除以$\sqrt{2}$,同求其差,再除以$\sqrt{2}$,剩下的一个数不变,经过两次这样的操作就又变成原来的三个数了,
即($\frac{m+n}{\sqrt{2}}$)2+($\frac{m-n}{\sqrt{2}}$)2+p2=m2+n2+p2,
∵32+(-4)2+(-1)2≠2012.
∴对a、b、c进行若干次操作后,不能使所得三个数的平方和等于2012.
点评 本题考查了对完全平方数的理解.拓展应用是解此题的关键,注意要打破思维常规进行分析.


科目:初中数学 来源: 题型:解答题
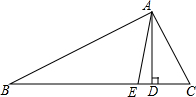 如图,三角形ABC中,∠C>∠B,AD是BC边上的高,AE是三角形中∠A的平分线.
如图,三角形ABC中,∠C>∠B,AD是BC边上的高,AE是三角形中∠A的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
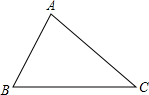 如图,利用尺规在平面内确定一点O,使得点O到△ABC的两边AB、AC的距离相等,并且点O到B、C两点的距离也相等(保留作图痕迹,不写作法).
如图,利用尺规在平面内确定一点O,使得点O到△ABC的两边AB、AC的距离相等,并且点O到B、C两点的距离也相等(保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
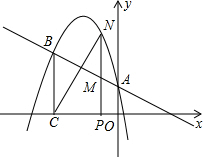 二次函数y=ax2+bx+c的图象经过点(-1,4),且与直线y=-$\frac{1}{2}$x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).
二次函数y=ax2+bx+c的图象经过点(-1,4),且与直线y=-$\frac{1}{2}$x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com