
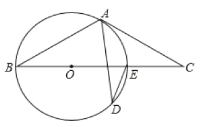
【题目】如图,AB是![]() 的直径,点C、D在
的直径,点C、D在![]() 上,且AD平分
上,且AD平分![]() ,过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F,G为AB的下半圆弧的中点,DG交AB于H,连接DB、GB.
,过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F,G为AB的下半圆弧的中点,DG交AB于H,连接DB、GB.
![]() 证明EF是
证明EF是![]() 的切线;
的切线;
![]() 求证:
求证:![]() ;
;
![]() 已知圆的半径
已知圆的半径![]() ,
,![]() ,求GH的长.
,求GH的长.
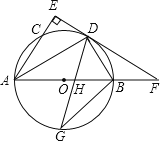
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】
(1)由题意可证OD∥AE,且EF⊥AE,可得EF⊥OD,即EF是⊙O的切线;(2)由同弧所对的圆周角相等,可得∠DAB=∠DGB,由余角的性质可得∠DGB=∠BDF;(3)由题意可得∠BOG=90°,根据勾股定理可求GH的长.
解:(1)证明:连接OD,
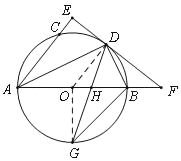
∵OA=OD,
∴∠OAD=∠ODA
又∵AD平分∠BAC,
∴∠OAD=∠CAD
∴∠ODA=∠CAD,
∴OD∥AE,
又∵EF⊥AE,
∴OD⊥EF,
∴EF是⊙O的切线
(2)∵AB是⊙O的直径,
∴∠ADB=90°
∴∠DAB+∠OBD=90°
由(1)得,EF是⊙O的切线,
∴∠ODF=90°
∴∠BDF+∠ODB=90°
∵OD=OB,
∴∠ODB=∠OBD
∴∠DAB=∠BDF
又∠DAB=∠DGB
∴∠DGB=∠BDF
(3)连接OG,
∵G是半圆弧中点,
∴∠BOG=90°
在Rt△OGH中,OG=5,OH=OB﹣BH=5﹣3=2.
∴GH=![]() =
=![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】完成下列各题:
(1)三根垂直地面的木杆甲、乙、丙,在路灯下乙、丙的影子如图1所示.试确定路灯灯泡的位置,再作出甲的影子.(不写作法,保留作图痕迹)

(2)如图2,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小型水库栏水坝的横断面是四边形ABCD,DC∥AB,测得迎水坡的坡角α=30°,已知背水坡的坡比为1.2:1,坝顶部DC宽为2m,坝高为6m,则坝底AB的长为_____m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼![]() (可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点
(可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点![]() 和点
和点![]() 处,
处,![]() 、
、![]() 均在
均在![]() 的中垂线上,且
的中垂线上,且![]() 、
、![]() 到大楼的距离分别为
到大楼的距离分别为![]() 米和
米和![]() 米,又已知
米,又已知![]() 长
长![]() 米,
米,![]() 长
长![]() 米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.
米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
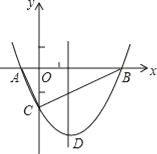
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在斜坡EF上有一信号发射塔CD,某兴趣小组想要测量发射塔CD的高度,于是在水平地面用仪器测得塔顶D的仰角为31°,已知仪器AB高为2m,斜坡EF的坡度为i=3:4,塔底距离坡底的距离CE=10m,最后测得塔高为12m,A、B、C、D、E在同一平面内,则仪器到坡底距离AE约为( )米(结果精确到0.1,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.6)

A. 18.6 B. 18.7 C. 22.0 D. 24.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是O的直径,点A和点D是0上的两点,过点A作⊙O的切线交BE延长线于点C.
(1)若∠ADE=25°,求∠C的度数;
(2)若AC=4,CE=2,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com