
【题目】已知二次函数![]() (a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3.
(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3.
(1)求A、B两点的坐标;
(2)若tan∠PDB=![]() ,求这个二次函数的关系式.
,求这个二次函数的关系式.
【答案】(1)A(![]() ,0);(2)
,0);(2)![]() .
.
【解析】
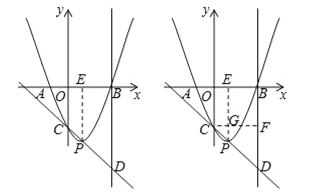
试题分析:(1)由二次函数的解析式可求出对称轴为x=1,过点P作PE⊥x轴于点E,所以OE:EB=CP:PD;
(2)过点C作CF⊥BD于点F,交PE于点G,构造直角三角形CDF,利用tan∠PDB=![]() 即可求出FD,由于△CPG∽△CDF,所以可求出PG的长度,进而求出a的值,最后将A(或B)的坐标代入解析式即可求出c的值.
即可求出FD,由于△CPG∽△CDF,所以可求出PG的长度,进而求出a的值,最后将A(或B)的坐标代入解析式即可求出c的值.
试题解析:(1)过点P作PE⊥x轴于点E,∵![]() ,∴该二次函数的对称轴为:x=1,∴OE=1
,∴该二次函数的对称轴为:x=1,∴OE=1
∵OC∥BD,∴CP:PD=OE:EB,∴OE:EB=2:3,∴EB=![]() ,∴OB=OE+EB=
,∴OB=OE+EB=![]() ,∴B(
,∴B(![]() ,0).
,0).
∵A与B关于直线x=1对称,∴A(![]() ,0);
,0);
(2)过点C作CF⊥BD于点F,交PE于点G,令x=1代入![]() ,∴y=c﹣a,令x=0代入
,∴y=c﹣a,令x=0代入![]() ,∴y=c,∴PG=a,∵CF=OB=
,∴y=c,∴PG=a,∵CF=OB=![]() ,∴tan∠PDB=
,∴tan∠PDB=![]() ,∴FD=2,∵PG∥BD,∴△CPG∽△CDF,∴
,∴FD=2,∵PG∥BD,∴△CPG∽△CDF,∴![]() ,∴PG=
,∴PG=![]() ,∴a=
,∴a=![]() ,∴
,∴![]() ,把A(
,把A(![]() ,0)代入
,0)代入![]() ,∴解得:c=﹣1,∴该二次函数解析式为:
,∴解得:c=﹣1,∴该二次函数解析式为:![]() .
.


科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
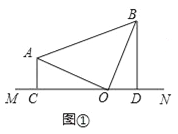
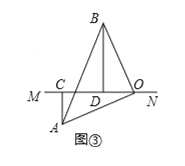
【题目】在△ABC中,∠AOB=90°,AO=BO,直线MN经过点O,且AC⊥MN于C,BD⊥MN于D
(1)当直线MN绕点O旋转到图①的位置时,求证:CD=AC+BD;
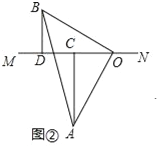
(2)当直线MN绕点O旋转到图②的位置时,求证:CD=AC﹣BD;
(3)当直线MN绕点O旋转到图③的位置时,试问:CD、AC、BD有怎样的等量关系?请写出这个等量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 过B(﹣2,6),C(2,2)两点.
过B(﹣2,6),C(2,2)两点.
(1)试求抛物线的解析式;
(2)记抛物线顶点为D,求△BCD的面积;
(3)若直线![]() 向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
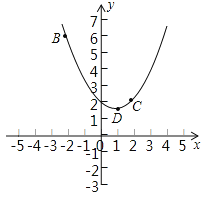
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com