
【题目】已知关于x的一元二次方程x2+(2m﹣1)x+m2=0有两个实数根x1和x2.
(1)求实数m的取值范围;
(2)当x12﹣x22=0时,求m的值.
【答案】(1)m≤![]() ;(2)m=
;(2)m=![]() .
.
【解析】
试题(1)若一元二次方程有两实数根,则根的判别式△=b2-4ac≥0,建立关于m的不等式,求出m的取值范围;
(2)由x12-x22=0得x1+x2=0或x1-x2=0;当x1+x2=0时,运用两根关系可以得到-2m-1=0或方程有两个相等的实根,据此即可求得m的值.
试题解析:(1)由题意有△=(2m-1)2-4m2≥0,
解得m≤![]() ,
,
即实数m的取值范围是m≤![]() ;
;
(2)由两根关系,得根x1+x2=-(2m-1),x1x2=m2,
由x12-x22=0得(x1+x2)(x1-x2)=0,
若x1+x2=0,即-(2m-1)=0,解得m=![]() ,
,
∵![]() >
>![]() ,
,
∴m=![]() 不合题意,舍去,
不合题意,舍去,
若x1-x2=0,即x1=x2
∴△=0,由(1)知m=![]() ,
,
故当x12-x22=0时,m=![]() .
.
考点: 1.根的判别式;2.根与系数的关系.


科目:初中数学 来源: 题型:
【题目】已知:三点A(-1,1),B(-3,2),C(-4,-1).

(1)作出与△ABC关于原点对称的△A1B1C1,并写出各顶点的坐标;
(2)作出与△ABC关于P(1,-2)点对称的△A2B2C2,并写出各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
【答案】y=﹣5x2+2x﹣1
【解析】试题分析:根据二次函数的定义得到m2+m﹣4=2且m﹣2≠0,由此求得m的值,进而得到该二次函数的解析式.
试题解析:依题意得:m2+m﹣4=2且m﹣2≠0. 即(m﹣2)(m+3)=0且m﹣2≠0,
解得m=﹣3,
则该二次函数的解析式为y=﹣5x2+2x﹣1
【题型】解答题
【结束】
21
【题目】如图,在ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=AD;③∠CHG=∠DAG;④HG=![]() AD.其中正确的有( )
AD.其中正确的有( )
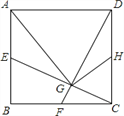
A. ① ② B. ① ② ④ C. ① ③ ④ D. ① ② ③ ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是正方形
是正方形![]() 对角线
对角线![]() 上一动点,点
上一动点,点![]() 在射线
在射线![]() 上,且
上,且![]() ,连接
,连接![]() ,
,![]() 为
为![]() 中点.
中点.
(1)如图1,当点![]() 在线段
在线段![]() 上时,试猜想
上时,试猜想![]() 与
与![]() 的数量关系和位置关系,并说明理由;
的数量关系和位置关系,并说明理由;

(2)如图2,当点![]() 在线段
在线段![]() 上时,(1)中的猜想还成立吗?请说明理由;
上时,(1)中的猜想还成立吗?请说明理由;

(3)如图3,当点![]() 在
在![]() 的延长线上时,请你在图3中画出相应的图形,并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.
的延长线上时,请你在图3中画出相应的图形,并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,再解决问题:
学习数轴之后,有同学发现在数轴上到两点之间距离相等的点,可以用表示这两点表示的数来确定.如:(1)到表示数4和数10距离相等的点表示的数是7,有这样的关系7=![]() (4+10);
(4+10);
(2)到表示数-3和数-7距离相等的点表示的数是-5,有这样的关系-5=![]() .
.
解决问题:根据上述规律完成下列各题:
(1)到表示数50和数150距离相等的点表示的数是_________
(2)到表示数![]() 和数
和数![]() 距离相等的点表示的数是__________
距离相等的点表示的数是__________
(3)到表示数![]() 12和数
12和数![]() 26距离相等的点表示的数是_________
26距离相等的点表示的数是_________
(4)到表示数a和数b距离相等的点表示的数是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
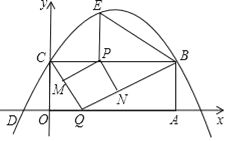
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE和Rt△OCD中的一个角相等?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数形结合思想回答下列问题:
(1)数轴上表示1和3两点之间的距离 .
(2)数轴上表示﹣12和﹣6的两点之间的距离是 .
(3)数轴上表示x和1的两点之间的距离表示为 .
(4)若x表示一个有理数,且﹣4<x<2,则|x﹣2|+|x+4|= .
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com