
【题目】如图,四边形ABCD中AB∥CD,对角线AC,BD相交于O,点E,F分别为BD上两点,且BE=DF,∠AEF=∠CFB.
(1)求证:四边形ABCD是平行四边形;
(2)若AC=2OE,试判断四边形AECF的形状,并说明理由.

【答案】(1)(2)见解析
【解析】试题分析:(1)已知AB∥CD,根据两直线平行,内错角相等可得∠ABD=∠CDB,由∠AEF=∠CFB,根据平角的定义可得∠AEB=∠CFD,利用ASA证得△ABE≌△CDF,根据全等三角形的性质可得AB=CD,由AB∥CD,根据一组对边平行且相等的四边形为平行四边形即可得四边形ABCD是平行四边形;(2)平行四边形AECF是矩形,根据平行四边形的性质可得OB=OD ,OA=OC=![]() AC,由BE=DF证得OE=OF,根据对角线互相平分的四边形为平行四边形可判定四边形AECF是平行四边形,再证得AC=EF,根据对角线相等的平行四边形是矩形即可判定平行四边形AECF是矩形.
AC,由BE=DF证得OE=OF,根据对角线互相平分的四边形为平行四边形可判定四边形AECF是平行四边形,再证得AC=EF,根据对角线相等的平行四边形是矩形即可判定平行四边形AECF是矩形.
试题解析:
(1)证明:∵AB∥CD,
∴∠ABD=∠CDB,
又∵∠AEF=∠CFB,
∴∠AEB=∠CFD,
又∵BE=DF,
∴△ABE≌△CDF(ASA),
∴AB=CD,
又∵AB∥CD,
∴四边形ABCD是平行四边形;
(2) 平行四边形AECF是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD ,OA=OC=![]() AC,
AC,
∵BE=DF,
∴OB﹣BE=DO﹣DF,
∴OE=OF,
又∵OA=OC,
∴四边形AECF是平行四边形,
又∵AC=2OE,EF=2OE,
∴AC=EF,
∴平行四边形AECF是矩形.


科目:初中数学 来源: 题型:
【题目】将背面相同,正面分别标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌面上,先从中随机的抽取一张卡片(不放回),将该卡片正面上的数字作为十位数字,再随机的抽取一张卡片,将该卡片正面上的数字作为个位数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中的图像(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为80.8千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.⑤汽车离出发地64千米是在汽车出发后1.2小时时。其中正确的说法共有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示,且顶点在网格格点上将△ABC向右平移7个单位长度,再向下平移2个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度),请解决下列问题:
(1)在图中画出平移后的△A1B1C1;
(2)直接写出点B1、C1的坐标:B1( , ),C1( , );
(3)填空:△ABC的面积是 (平方单位).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(﹣2,0),C(2,2),过C作CB⊥x轴于B.

(1)如图1,△ABC的面积是 ;
(2)如图1,在y轴上找一点P,使得△ABP的面积与△ABC的面积相等,请直接写出P点坐标: ;
(3)如图2,若过B作BD∥AC交y轴于D,则∠BAC+∠ODB的度数为 度;
(4)如图3,BD∥AC,若AE、DE分别平分∠CAB,∠ODB,求∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
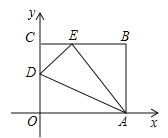
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com