
 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C'顺时针旋转90°,得到△A″B″C′,
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C'顺时针旋转90°,得到△A″B″C′,分析 (1)先利用网格特点和平移的性质画出点A、B、C平移后的对应点A′、B′、C′,从而得到△A′B′C′,然后利用网格特点和旋转的性质画出点A′、C′的对应点A″、B″,从而得到△A″B″C′;
(2)先利用勾股定理计算A′C′,由于线段A′C′在旋转过程中所扫过的部分为以C′为圆心,A′C′为半径,圆心角为90°的扇形,于是根据扇形面积公式可计算出线段A′C′在旋转过程中所扫过的面积.
解答 解:(1)如图,△A′B′C′和△A″B″C′为所作;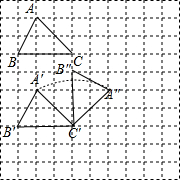
(2)A′C′=$\sqrt{2^2+2^2}$=2$\sqrt{2}$,
所以线段A′C′在旋转过程中所扫过的面积=$\frac{90π}{360}$×(2$\sqrt{2}$)2=2π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.


科目:初中数学 来源: 题型:选择题
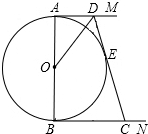 如图,AB是⊙O的直径,AM和BN是它的两条切线,DC切⊙O于E,交AM于D,交BN于C.若AD•BC=9,则直径AB的长为( )
如图,AB是⊙O的直径,AM和BN是它的两条切线,DC切⊙O于E,交AM于D,交BN于C.若AD•BC=9,则直径AB的长为( )| A. | 3$\sqrt{2}$ | B. | 6 | C. | 9 | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
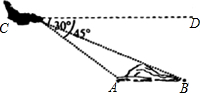 钓鱼岛及周边岛屿自古以来就是中国的领土.如图,我海监飞机在距海平面高度为2千米的C处测得钓鱼岛南北两端A、B的俯角∠DCA=45°、∠DCB=30°(己知A、B、C三点在同一平面上),求钓鱼岛南北两端A、B的距离.(参考数据:$\sqrt{3}$=1.73)
钓鱼岛及周边岛屿自古以来就是中国的领土.如图,我海监飞机在距海平面高度为2千米的C处测得钓鱼岛南北两端A、B的俯角∠DCA=45°、∠DCB=30°(己知A、B、C三点在同一平面上),求钓鱼岛南北两端A、B的距离.(参考数据:$\sqrt{3}$=1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
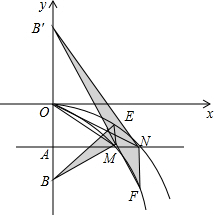 如图,在平面直角坐标系中,点A(0,-a2)(a>0)在y轴的负半轴上,过点A作x轴的平行线,分别交抛物线C1:y=-$\frac{1}{2}$x2(x>0)于点M,交抛物线C2:y=-$\frac{1}{4}{x}^{2}$(x>0)于点N,连接OM,ON.
如图,在平面直角坐标系中,点A(0,-a2)(a>0)在y轴的负半轴上,过点A作x轴的平行线,分别交抛物线C1:y=-$\frac{1}{2}$x2(x>0)于点M,交抛物线C2:y=-$\frac{1}{4}{x}^{2}$(x>0)于点N,连接OM,ON.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
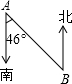 石家庄现在正在修建的地铁1号线大致是东西走向的,已知在白佛站往东有一个拐弯,现记弯道的两个端点分别为A,B,如图所示,若在A地测得地铁隧道的走向是南偏东46°,则为了使地铁隧道能够准确接通,在B地施工的地铁隧道的走向应为( )
石家庄现在正在修建的地铁1号线大致是东西走向的,已知在白佛站往东有一个拐弯,现记弯道的两个端点分别为A,B,如图所示,若在A地测得地铁隧道的走向是南偏东46°,则为了使地铁隧道能够准确接通,在B地施工的地铁隧道的走向应为( )| A. | 北偏西46° | B. | 北偏西44° | C. | 南偏东46° | D. | 南偏西44° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com