
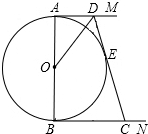
 如图,AB是⊙O的直径,AM和BN是它的两条切线,DC切⊙O于E,交AM于D,交BN于C.若AD•BC=9,则直径AB的长为( )
如图,AB是⊙O的直径,AM和BN是它的两条切线,DC切⊙O于E,交AM于D,交BN于C.若AD•BC=9,则直径AB的长为( )| A. | 3$\sqrt{2}$ | B. | 6 | C. | 9 | D. | $\sqrt{13}$ |
分析 先证明∠DOC=90°,再证明△AOD∽△BCO得OA2=AD•BC,由此即可解决问题.
解答 解: 如图,连接OC.
如图,连接OC.
∵AM和BN是它的两条切线,
∴AM⊥AB,BN⊥AB,
∴AM∥BN,
∴∠ADE+∠BCE=180°
∵DC切⊙O于E,
∴∠ODE=$\frac{1}{2}$∠ADE,∠OCE=$\frac{1}{2}$∠BCE,
∴∠ODE+∠OCE=90°,
∴∠DOC=90°,
∴∠AOD+∠COB=90°,
∵∠AOD+∠ADO=90°,
∴∠AOD=∠OCB,
∵∠OAD=∠OBC=90°,
∴△AOD∽△BCO,
∴$\frac{AD}{BO}=\frac{AO}{BC}$,
∴OA2=AD•BC=9,
∴OA=3,
∴AB=2•OA=6.
故选B.
点评 本题考查切线的性质、平行线的性质、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形,利用相似三角形性质解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.68×104 | B. | 1.68×106 | C. | 1.68×107 | D. | 0.168×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
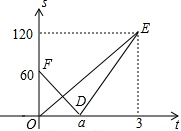 甲、乙两辆遥控车沿直线AC作同方向的匀速运动,甲、乙同时分别从A、B出发,沿轨道到达C处,已知甲的速度是乙的速度的1.5倍,设t分钟后甲、乙两车与B处距离分别为S1,S2,函数关系如图所示,当两车的距离小于10米时,信号会产生相互干扰,那么t是下列哪个值时两车的信号会相互干扰( )
甲、乙两辆遥控车沿直线AC作同方向的匀速运动,甲、乙同时分别从A、B出发,沿轨道到达C处,已知甲的速度是乙的速度的1.5倍,设t分钟后甲、乙两车与B处距离分别为S1,S2,函数关系如图所示,当两车的距离小于10米时,信号会产生相互干扰,那么t是下列哪个值时两车的信号会相互干扰( )| A. | $\frac{2}{3}$ | B. | 2 | C. | $\frac{11}{5}$ | D. | $\frac{13}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C'顺时针旋转90°,得到△A″B″C′,
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C'顺时针旋转90°,得到△A″B″C′,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com