
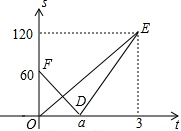
 甲、乙两辆遥控车沿直线AC作同方向的匀速运动,甲、乙同时分别从A、B出发,沿轨道到达C处,已知甲的速度是乙的速度的1.5倍,设t分钟后甲、乙两车与B处距离分别为S1,S2,函数关系如图所示,当两车的距离小于10米时,信号会产生相互干扰,那么t是下列哪个值时两车的信号会相互干扰( )
甲、乙两辆遥控车沿直线AC作同方向的匀速运动,甲、乙同时分别从A、B出发,沿轨道到达C处,已知甲的速度是乙的速度的1.5倍,设t分钟后甲、乙两车与B处距离分别为S1,S2,函数关系如图所示,当两车的距离小于10米时,信号会产生相互干扰,那么t是下列哪个值时两车的信号会相互干扰( )| A. | $\frac{2}{3}$ | B. | 2 | C. | $\frac{11}{5}$ | D. | $\frac{13}{5}$ |
分析 先求出s与t的关系式,再根据两车的距离,列出不等式,解不等式可得答案.
解答 解:乙的速度v2=120÷3=40(米/分),甲的速度v甲=40×1.5=60米/分.
所以a=$\frac{60}{60}$=1分.
设函数解析式为d1=kt+b,
0≤t≤1时,把(0,60)和(1,0)代入得d1=-60t+60,
1<t≤3时,把(1,0)和(3,120)代入得d1=60t-60;
d2=40t,
当0≤t<1时,d2+d1<10,
即-60t+60+40t<10,
解得t>2.5,
因为0≤t<1,
所以当0≤t<1时,两遥控车的信号不会产生相互干扰;
当1≤t≤3时,d2-d1<10,
即40t-(60t-60)<10,
所以t>2.5,
当2.5<t≤3时,两遥控车的信号会产生相互干扰.
故选D.
点评 本题考查了一次函数的应用,解题关键是利用待定系数法确定函数解析式,理解路程、速度、时间三者的关系,学会分类讨论的思想,转化的思想,把问题转化为不等式解决,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 28分,28分 | B. | 30分,28分 | C. | 28分,27.5分 | D. | 30分,27.5分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
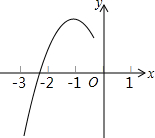 已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:| A. | ②③ | B. | ①③ | C. | ①②③ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
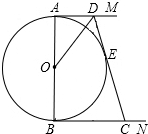 如图,AB是⊙O的直径,AM和BN是它的两条切线,DC切⊙O于E,交AM于D,交BN于C.若AD•BC=9,则直径AB的长为( )
如图,AB是⊙O的直径,AM和BN是它的两条切线,DC切⊙O于E,交AM于D,交BN于C.若AD•BC=9,则直径AB的长为( )| A. | 3$\sqrt{2}$ | B. | 6 | C. | 9 | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进价(元/千克) | 售价(元/千克) | |
| 苹果 | 5 | 8 |
| 丑桔 | 9 | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
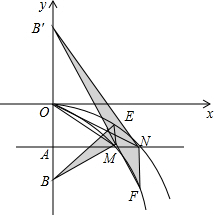 如图,在平面直角坐标系中,点A(0,-a2)(a>0)在y轴的负半轴上,过点A作x轴的平行线,分别交抛物线C1:y=-$\frac{1}{2}$x2(x>0)于点M,交抛物线C2:y=-$\frac{1}{4}{x}^{2}$(x>0)于点N,连接OM,ON.
如图,在平面直角坐标系中,点A(0,-a2)(a>0)在y轴的负半轴上,过点A作x轴的平行线,分别交抛物线C1:y=-$\frac{1}{2}$x2(x>0)于点M,交抛物线C2:y=-$\frac{1}{4}{x}^{2}$(x>0)于点N,连接OM,ON.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com