
【题目】四边形ABCD中,E是AB边上的一个动点(不与点A、B重合),连接DE,过点E作EP⊥DE.
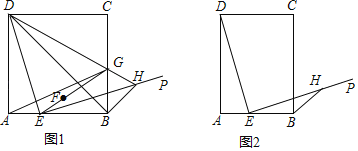
(1)如图1,当四边形ABCD是正方形时,点A关于直线DE的对称点为点F,连接EF并延长交BC于点G;射线DG交EP于点H,连接BH.
①求证:GF=GC
②请求出![]() 的值;
的值;
(2)如图2,四边形ABCD是矩形,且AD=kAB,点H是射线EP上的一点,连接BH,当DE=kEH时,请直接写出![]() 的值.
的值.
【答案】(1)①详见解析;②![]() ;(2)
;(2)![]() .
.
【解析】
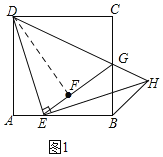
(1)①如图1,连接DF,根据对称得:△ADE≌△FDE,再由HL证明Rt△DFG≌Rt△DCG,即可得出结论;
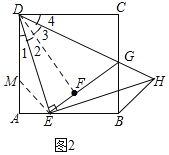
②如图2,作辅助线,构建AM=AE,先证明∠EDG=45°,得DE=EH,证明△DME≌△EBH,则EM=BH,根据等腰直角的性质得:EM=![]() AE,即可得出结论;
AE,即可得出结论;
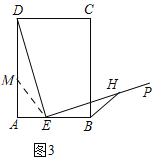
(2)先构建AM=kAE,进而得出![]() =k,即可得出
=k,即可得出![]() ,进而判断出△MDE∽△BEH,得出
,进而判断出△MDE∽△BEH,得出![]() =k,再判断出ME=
=k,再判断出ME=![]() AE,即可得出结论.
AE,即可得出结论.
证明:(1)①如图1,连接DF,
∵四边形ABCD是正方形,
∴DA=DC,∠A=∠C=90°,
∵点A关于直线DE的对称点为F,
∴△ADE≌△FDE,
∴DA=DF=DC,∠DFE=∠A=90°,
∴∠DFG=90°,
在Rt△DFG和Rt△DCG中,
∵![]() ,
,
∴Rt△DFG≌Rt△DCG(HL),
∴GF=GC;
②如图2,在线段AD上截取AM,使AM=AE,
∵AD=AB,
∴DM=BE,
由①知:∠1=∠2,∠3=∠4,
∵∠ADC=90°,
∴∠1+∠2+∠3+∠4=90°,
∴2∠2+2∠3=90°,
∴∠2+∠3=45°,
即∠EDG=45°,
∵EH⊥DE,
∴∠DEH=90°,△DEH是等腰直角三角形,
∴∠AED+∠BEH=∠AED+∠1=90°,DE=EH,
∴∠1=∠BEH,
在△DME和△EBH中,
∵ ,
,
∴△DME≌△EBH(SAS),
∴EM=BH,
Rt△AEM中,∠A=90°,AM=AE,
∴EM=![]() AE,
AE,
∴BH=![]() AE,
AE,
∴![]() =
=![]() ;
;
(2)如图3,
在AD上截取AM,使AM=kAE,
∵AD=kAB,
∴DM=AD﹣AM=kAB﹣kAE=k(AB﹣AE)=kBE,
∴![]() =k
=k
∵DE=kEH,
∴![]() =k,
=k,
∴![]() ,
,
同①的方法得,∠MDE=∠BEH,
∴△MDE∽△BEH,
∴![]() =k,
=k,
在Rt△EAM中,ME=![]() ,
,
∴![]() ,
,
∴![]() =
=![]() .
.


科目:初中数学 来源: 题型:
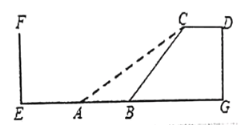
【题目】速滑运动受到许多年轻人的喜爱。如图,四边形![]() 是某速滑场馆建造的滑台,已知
是某速滑场馆建造的滑台,已知![]() ,滑台的高
,滑台的高![]() 为
为![]() 米,且坡面
米,且坡面![]() 的坡度为
的坡度为![]() .后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为
.后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为![]() .
.
(1)求新坡面![]() 的坡角及
的坡角及![]() 的长;
的长;
(2)原坡面底部![]() 的正前方
的正前方![]() 米处
米处![]() 是护墙
是护墙![]() ,为保证安全,体育管理部门规定,坡面底部至少距护墙
,为保证安全,体育管理部门规定,坡面底部至少距护墙![]() 米。请问新的设计方案能否通过,试说明理由(参考数据:
米。请问新的设计方案能否通过,试说明理由(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
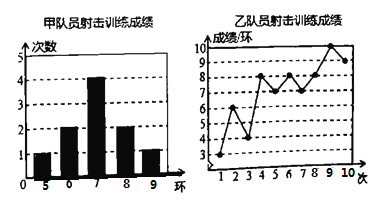
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)写出表格中![]() 的值:
的值:
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在7×7正方形网格中的每个小正方形边长都为1个单位长度,我们把每个小正方形的顶点称为格点,点A、B、C都为格点,且点A(1,2),请分别仅用一把无刻度的直尺画图;
(1)过点C画一条线段AB的平行线段CD,直接写出格点D的坐标;
(2)过点C画一条线段AB的垂直线段CE,直接写出格点E的坐标;
(3)作∠DCE的角平分线CF,直接写出格点F的坐标;
(4)作∠ABM,使∠ABM=45°,直接写出格点M的坐标;
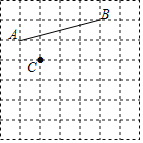
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每一个小正方形的边长均为 1.格点三角形 ABC(顶点是网格线交点的三角形)的顶点 A、C 的坐标分别是(﹣2,0),(﹣3,3).
(1)请在图中的网格平面内建立平面直角坐标系,写出点 B 的坐标;
(2)把△ABC 绕坐标原点 O 顺时针旋转 90°得到△A1B1C1,画出△A1B1C1,写出点
B1的坐标;
(3)以坐标原点 O 为位似中心,相似比为 2,把△A1B1C1 放大为原来的 2 倍,得到△A2B2C2 画出△A2B2C2,使它与△AB1C1 在位似中心的同侧;
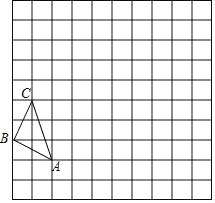
请在 x 轴上求作一点 P,使△PBB1 的周长最小,并写出点 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】判断关于x的方程mx2+(2m﹣1)x+m+3=0的根的情况,并直接写出关于x的方程mx2+(2m﹣1)x+m+3=0的根及相应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中不正确的是( )
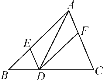
A.四边形AEDF是平行四边形
B.若∠BAC=90°,则四边形AEDF是矩形
C.若AD平分∠BAC,则四边形AEDF是矩形
D.若AD⊥BC且AB=AC,则四边形AEDF是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com