
����Ŀ����֪��OΪ��ABC�����Բ��Բ��O��AB�ϣ� SA'>�����ԣ�����Ϊ�����ݹ���ÿһ������Ե�10�֣��������20�֣��������÷�Ҳ���۷֣�
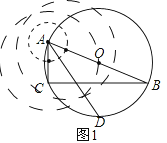
��1����ͼ1�У��ó߹���ͼ����BAC��ƽ����AD����O��D��������ͼ�ۼ�����д������֤������
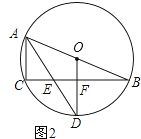
��2����ͼ2�����BAC��ƽ����AD��BC��E����O�뾶Ϊ5��AC=4������OD��BC��F������֤��OD��BC������EF�ij���
���𰸡�
��1��
�⣺�߹���ͼ��ͼ1��ʾ��
��2��
�⣺����ͼ2����ADƽ�֡�BAC��
���DAC=��BAD��
��OA=OD��
���OAD=��D��
���CAD=��D��
��AC��OD��
���ACB=��OFB��
��AB��ֱ����
���ACB=90�㣬
���OFB=90�㣬
��OD��BC��
�ڡ�AC��OD��
��![]() ����
����![]() ��
��
��OF=2��
��FD=5��2=3��
��RT��OFB��BF=![]() ��
��
��OD��BC��
��CF=BF=![]() ��
��
��AC��OD��
���EFD�ס�ECA��
��![]() ��
��
��![]() ��
��
��EF=![]() CF=
CF=![]() ��
��![]() =
=![]() ��
��
����������1����������ƽ���ߵķ����������ɣ�
��2���������AC��OD��Ȼ�����Բ�ܽǶ�����á�ACB=90�㣬����֤�ã��ڸ��ݹ��ɶ������BF����CF�ij���Ȼ�����ƽ���߷��߶γɱ����������![]() ���������
���������![]() ���̶����EF�ij���
���̶����EF�ij���
�����㾫�������չ��ɶ����ĸ����Բ�ܽǶ����ǽ����ĸ�������Ҫ֪��ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��������Բ���ϵĽǽ���Բ�Ľ�;������Բ���ϣ����������߷ֱ���Բ����һ������Ľǽ���Բ�ܽ�;һ�������Ե�Բ�ܽǵ��������Ե�Բ�Ľǵ�һ�룮


 53���ò�ϵ�д�
53���ò�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��G��E�ֱ���������ABCD�ı�AB��BC�ĵ㣬��AG=CE��AE��EF��AE=EF���������½��ۣ�
��BE=![]() GE�� �ڡ�AGE�ա�ECF�� �ۡ�FCD=45�㣻 �ܡ�GBE�ס�ECH�����У���ȷ�Ľ����У�������
GE�� �ڡ�AGE�ա�ECF�� �ۡ�FCD=45�㣻 �ܡ�GBE�ס�ECH�����У���ȷ�Ľ����У�������
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�E��AD�ߵ��е㣬BE��AC�ڵ�F������DF����������������ۣ��١�AEF�ס�CAB����CF=2AF����DF=DC����tan��CAD=![]() ����S�ı���CDEF=
����S�ı���CDEF=![]() S��ABF �� ������ȷ�Ľ����У�������
S��ABF �� ������ȷ�Ľ����У�������
A.5��
B.4��
C.3��
D.2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AΪij���ξ�������ѹ۾��㣬�οͿɴ�B�������³��ȵ���С�۾�ƽ̨DE�۾���Ȼ������E�����������³�����A��������ʱ��A��������������ֱ�ӵ���C������֪��AC��BC��C��DE��BC��BC=110�ף�DE=9�ף�BD=60�ף���=32�㣬��=68�㣬��AC�ĸ߶ȣ����ο����ݣ�sin32���0.53��cos32���0.85��tan32���0.62��sin68���0.93��cos68���0.37��tan68���2.48��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Сǿ��С�������桰������ʯͷ��������Ϸ���������һ�Σ�������ƽ�ֵĸ���Ϊ��������
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+3�ĶԳ�����ֱ��x=1��
��1����֤��2a+b=0
��2��������x�ķ���ax2+bx��8=0��һ����Ϊ4���̵���һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ˮƽ������������һ��ǽAB��ǽ����һյ·��D������DCǡ��ͨ��ǽ����ߵ�B����������γ�37��ǣ�ǽ�ڵƹ��µ�Ӱ��Ϊ�߶�AC�������AC=5.5�ף�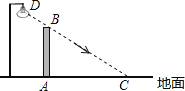
��1����ǽAB�ĸ߶ȣ������ȷ��0.1�ף������ο����ݣ�tan37���0.75��sin37���0.60��cos37���0.80��
��2�����Ҫ����Ӱ��AC�ij��ȣ�ͬʱ���ܸı�ǽ�ĸ߶Ⱥ�λ�ã�����д�����ֲ�ͬ�ķ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=3��BC=5����P��BC���ϵ�һ�����㣨��P���B��C�����غϣ����ֽ���PCD��ֱ��PD�۵���ʹ��C�䵽��F��������P����BPF�Ľ�ƽ���߽�AB�ڵ�E����BP=x��BE=y��������ͼ���У��ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ�������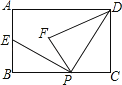
A.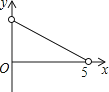
B.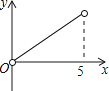
C.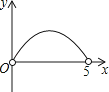
D.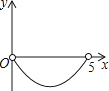
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com