
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,设AB=c,BC=a,AC=b,中线AE,BF相交于G,若AE⊥BF.
(1)①当∠ABF=60°,c=4时,求a与b的值;
②当∠ABF=30°,c=2 ![]() 时,a= , b=;
时,a= , b=;
(2)由(1)获得启示,猜想a2 , b2 , c2三者之间满足数量关系式是;(直接写出结果)
(3)如图2,在平行四边形ABCD中,AB=4 ![]() ,BC=3
,BC=3 ![]() ,点E,F,G分别是AD,AB,CD的中点,CF与BG交于P点,若EF⊥FC.利用(2)中的结论,求BG的长.
,点E,F,G分别是AD,AB,CD的中点,CF与BG交于P点,若EF⊥FC.利用(2)中的结论,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,CO⊥AB于O,D在⊙O上,连接BD,CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.
(1)求证:FD是⊙O的切线;
(2)若AF=8,tan∠BDF=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
乙校成绩统计表
分数(分) | 人数(人) |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
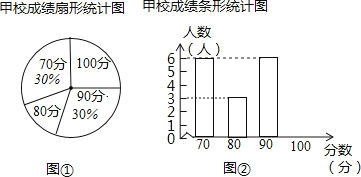
(1)在图①中,“80分”所在扇形的圆心角度数为 ;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自从2012年12月4日中央公布“八项规定”以来,我市某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果绘制了如下统计表和统计图,根据所提供的信息回答下列问题:
选项 | 频数 | 频率 |
A | 30 | M |
B | n | 0.2 |
C | 5 | 0.1 |
D | 5 | 0.1 |

(1)这次被抽查的学生有多少人?
(2)求表中m,n的值,并补全条形统计图;
(3)该中学有学生2200名,请估计这餐晚饭有剩饭的学生人数,按平均每人剩10克米饭计算,这餐晚饭将浪费多少千克米饭?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O为△ABC的外接圆,圆心O在AB上. SA'>”不对,理由为:根据规则:每一题抢答对得10分,抢答错扣20分,抢答不到不得分也不扣分.
(1)在图1中,用尺规作图作∠BAC的平分线AD交⊙O于D(保留作图痕迹,不写作法与证明);
(2)如图2,设∠BAC的平分线AD交BC于E,⊙O半径为5,AC=4,连接OD交BC于F.①求证:OD⊥BC;②求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中.顶点为(﹣4,﹣1)的抛物线交y轴于点A(0,3),交x轴于B,C两点.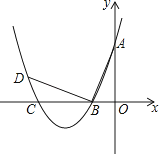
(1)求此抛物线的解析式;
(2)已知点P是抛物线上位于B,C两点之间的一个动点,问:当点P运动到什么位置时,四边形ABPC的面积最大?并求出此时四边形ABPC的面积.
(3)过点B作AB的垂线交抛物线于点D,是否存在以点C为圆心且与线段BD和抛物线的对称轴l同时相切的圆?若存在,求出圆的半径;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com