
【题目】如图,AB为⊙O的直径,CO⊥AB于O,D在⊙O上,连接BD,CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.
(1)求证:FD是⊙O的切线;
(2)若AF=8,tan∠BDF=![]() ,求EF的长.
,求EF的长.
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+4的图象与反比例y= ![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点. 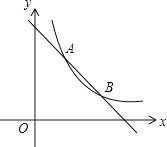
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE=![]() GE; ②△AGE≌△ECF; ③∠FCD=45°; ④△GBE∽△ECH,其中,正确的结论有( )
GE; ②△AGE≌△ECF; ③∠FCD=45°; ④△GBE∽△ECH,其中,正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为![]() 米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
(1)求测速点M到该公路的距离;
(2)通过计算判断此车是否超速.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
A.6
B.8
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市团委在2015年3月初组成了300个学雷锋小组,现从中随机抽取6个小组在3月份做好事件数的统计情况如图所示:
(1)这6个学雷锋小组在2015年3月份共做好事多少件?
(2)补全条形统计图;
(3)请估计该市300个学雷锋小组在2015年3月份共做好事多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() ;⑤S四边形CDEF=
;⑤S四边形CDEF=![]() S△ABF , 其中正确的结论有( )
S△ABF , 其中正确的结论有( )
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.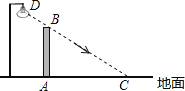
(1)求墙AB的高度(结果精确到0.1米);(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)
(2)如果要缩短影子AC的长度,同时不能改变墙的高度和位置,请你写出两种不同的方法
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com