
【题目】如图,一次函数y=﹣x+4的图象与反比例y= ![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点. 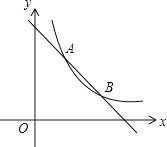
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求PA+PB的最小值.
【答案】
(1)解:把点A(1,a)代入一次函数y=﹣x+4,
得a=﹣1+4,
解得a=3,
∴A(1,3),
点A(1,3)代入反比例函数y= ![]() ,
,
得k=3,
∴反比例函数的表达式y= ![]() ,
,
两个函数解析式联立列方程组得  ,
,
解得x1=1,x2=3,
∴点B坐标(3,1)
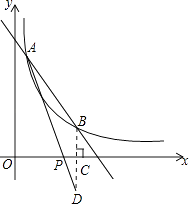
(2)解:作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB=PA+PD=AD的值最小,
∴D(3,﹣1),
∵A(1,3),
∴AD= ![]() =2
=2 ![]() ,
,
∴PA+PB的最小值为2 ![]() .
.
【解析】(1)把点A(1,a)代入一次函数y=﹣x+4,即可得出a,再把点A坐标代入反比例函数y= ![]() ,即可得出k,两个函数解析式联立求得点B坐标;(2)作点B作关于x轴的对称点D,连接AD,交x轴于点P,此时PA+PB=PA+PD=AD的值最小,然后根据勾股定理即可求得.
,即可得出k,两个函数解析式联立求得点B坐标;(2)作点B作关于x轴的对称点D,连接AD,交x轴于点P,此时PA+PB=PA+PD=AD的值最小,然后根据勾股定理即可求得.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2x+1)x+k2=0①有两个不相等的实数根.
(1)求k的取值范围;
(2)设方程①的两个实数根分别为x1 , x2 , 当k=1时,求x12+x22的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使DE=CG,连接AE、CD. 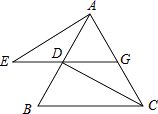
(1)求证:△AGE≌△DAC;
(2)过E做EF∥DC.交BC于F.连接AF.判断△AEF是怎样的三角形.并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是某手机店1~4月份的统计图,分析统计图,对3、4月份三星手机的销售情况四个同学得出的以下四个结论,其中正确的为( ) 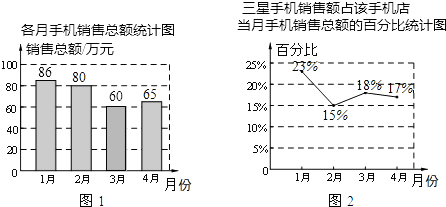
A.4月份三星手机销售额为65万元
B.4月份三星手机销售额比3月份有所上升
C.4月份三星手机销售额比3月份有所下降
D.3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位射击运动员在10次射击训练中,命中靶的环数如图.
请你根据图表,完成下列问题:
(1)
射击序次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩/环 | 8 | 10 | 7 | 9 | 10 | 7 | 10 |
(2)求该运动员这10次射击训练的平均成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,设AB=c,BC=a,AC=b,中线AE,BF相交于G,若AE⊥BF.
(1)①当∠ABF=60°,c=4时,求a与b的值;
②当∠ABF=30°,c=2 ![]() 时,a= , b=;
时,a= , b=;
(2)由(1)获得启示,猜想a2 , b2 , c2三者之间满足数量关系式是;(直接写出结果)
(3)如图2,在平行四边形ABCD中,AB=4 ![]() ,BC=3
,BC=3 ![]() ,点E,F,G分别是AD,AB,CD的中点,CF与BG交于P点,若EF⊥FC.利用(2)中的结论,求BG的长.
,点E,F,G分别是AD,AB,CD的中点,CF与BG交于P点,若EF⊥FC.利用(2)中的结论,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,CO⊥AB于O,D在⊙O上,连接BD,CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.
(1)求证:FD是⊙O的切线;
(2)若AF=8,tan∠BDF=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com