
����Ŀ����ͼ1���ڡ�ABC�У���AB=c��BC=a��AC=b������AE��BF�ཻ��G����AE��BF��
��1���ٵ���ABF=60�㣬c=4ʱ����a��b��ֵ��
�ڵ���ABF=30�㣬c=2 ![]() ʱ��a= �� b=��
ʱ��a= �� b=��
��2���ɣ�1�������ʾ������a2 �� b2 �� c2����֮������������ϵʽ������ֱ��д�������
��3����ͼ2����ƽ���ı���ABCD�У�AB=4 ![]() ��BC=3
��BC=3 ![]() ����E��F��G�ֱ���AD��AB��CD���е㣬CF��BG����P�㣬��EF��FC�����ã�2���еĽ��ۣ���BG�ij���
����E��F��G�ֱ���AD��AB��CD���е㣬CF��BG����P�㣬��EF��FC�����ã�2���еĽ��ۣ���BG�ij���
���𰸡�
��1��![]() ��
��![]()
��2��a2+b2=5c2
��3��
�⣺ȡBC���е�H������HG��DB����ͼ2��
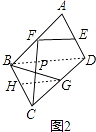
��E��F��G�ֱ���AD��AB��CD���е㣬
��EF��DB��HG��
��BF��CG��BF=CG��
���BFP=��GCP��
�ڡ�BFP���PCG�У�  ��
��
���BFP�ա�PCG��
��PF=CP��
��P��BG���е㣬
�֡�EF��FC��
��HG��PC��
�ɣ�2����֪BC2+BG2=5CG2��
��AB=4 ![]() ��BC=3
��BC=3 ![]() ��
��
�ࣨ3 ![]() ��2+BG2=5��2
��2+BG2=5��2 ![]() ��2��
��2��
��BG= ![]() ��
��
���������⣺��1���١�AE��BF����ABF=60�㣬AB=4��
����Rt��ABG��BG= ![]() AB=2��AG=ABcos60��=2
AB=2��AG=ABcos60��=2 ![]() ��
��
��AE��BF�ǡ�ABC�����ߣ�
��FG= ![]() BG=1a2+b2=5c2
BG=1a2+b2=5c2
��Rt��AGF��AF= ![]() =
= ![]() ��
��
��AC=b=2 ![]() ��
��
ͬ���ɵ�BC=a=2 ![]() ��
��
�ڵ���ABF=30�㣬AB=2 ![]() ��
��
����Rt��ABG��AG= ![]() AB=
AB= ![]() ��BG=ABcos30��=3��
��BG=ABcos30��=3��
��FG= ![]() BG=
BG= ![]() ��
��
��Rt��AGF��AF= ![]() =
= ![]() ��
��
��AC=b= ![]() ��
��
ͬ����BC=a= ![]() ��
��
���Դ��ǣ� ![]() ��
�� ![]() ����2�����룺a2+b2=5c2 ��
����2�����룺a2+b2=5c2 ��
�ɢٿ�֪��a2=28��b2=52��c2=16��
��a2+b2=52+28=80=5��16=5c2 ��
��a2+b2=5c2 ��
�ɢڿ�֪��a2=39��b2=21��c2=12��
��a2+b2=39+21=60=5��12=5c2 ��
��a2+b2=5c2 ��
���Դ���a2+b2=5c2��
�����㾫����ͨ���������ƽ���ı��ε����ʣ�����ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�ּ����Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���BAC=60�㣬��ABC=45�㣬AB=2 ![]() ��D���߶�BC�ϵ�һ�����㣬��ADΪֱ������O�ֱ�AB��AC��E��F������EF�����߶�EF���ȵ���СֵΪ ��
��D���߶�BC�ϵ�һ�����㣬��ADΪֱ������O�ֱ�AB��AC��E��F������EF�����߶�EF���ȵ���СֵΪ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=��x+4��ͼ���뷴����y= ![]() ��kΪ��������k��0����ͼ����A��1��a����B���㣮
��kΪ��������k��0����ͼ����A��1��a����B���㣮 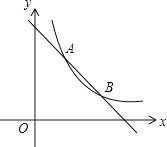
��1�����������ı���ʽ����B�����ꣻ
��2����x������һ��P��ʹPA+PB��ֵ��С����PA+PB����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=a��x��m��2+2m��2������m��1������ΪP����y���ཻ�ڵ�A��0��m��1�������Ӳ��ӳ�PA��PO�ֱ���x�ᡢ�����߽��ڵ�B��C������BC������PBC�Ƶ�P��ʱ����ת�á�PB��C�䣬ʹ��C�����������������ϣ�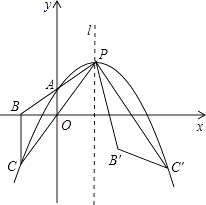
��1���������ߵĽ���ʽΪ���ú�m��ʽ�ӱ�ʾ����
��2����֤��BC��y�
��3������B��ǡ�������߶�BC���ϣ����ʱm��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ο���ʵ����У���ʦҪ��ͬѧ�����ò���Ǻ�Ƥ�߹����ѧ¥AB�ĸ߶ȣ�ͬѧ���ڽ�ѧ¥����ǰ��D���ø�Ϊ1�IJ���Dz�Ľ�ѧ¥����A������Ϊ30�㣬Ȼ���������ѧ¥����ǰ��30����E�����ֲ��A������Ϊ60�㣬���ѧ¥�߶�AB�Ƕ����ף�����ȷ��0.1�ף��ο����� ![]() =1.732��
=1.732��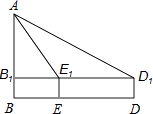
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA����1��1����B����3��1����C����1��4����
��1��������ABC����y��ԳƵġ�A1B1C1��
��2������ABC���ŵ�B˳ʱ����ת90���õ���A2BC2 �� ����ͼ�л�����A2BC2 �� ������߶�BC��ת��������ɨ�����������������У���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��G��E�ֱ���������ABCD�ı�AB��BC�ĵ㣬��AG=CE��AE��EF��AE=EF���������½��ۣ�
��BE=![]() GE�� �ڡ�AGE�ա�ECF�� �ۡ�FCD=45�㣻 �ܡ�GBE�ס�ECH�����У���ȷ�Ľ����У�������
GE�� �ڡ�AGE�ա�ECF�� �ۡ�FCD=45�㣻 �ܡ�GBE�ס�ECH�����У���ȷ�Ľ����У�������
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݵ�·�����涨���ں���ij�α�ֱ��·����ʻ�ij���������40ǧ��/ʱ����֪�������ٵ�M���ù�·A��ľ���Ϊ![]() �ף���MAB=45�㣬��MBA=30�㣨��ͼ��ʾ��������һ��������A��B����������ʻ����ô˳���A����ʻ��B�����õ�ʱ��Ϊ3�룮
�ף���MAB=45�㣬��MBA=30�㣨��ͼ��ʾ��������һ��������A��B����������ʻ����ô˳���A����ʻ��B�����õ�ʱ��Ϊ3�룮
��1������ٵ�M���ù�·�ľ��룻
��2��ͨ�������жϴ˳��Ƿ��٣����ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��![]() ��2.24��
��2.24��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AΪij���ξ�������ѹ۾��㣬�οͿɴ�B�������³��ȵ���С�۾�ƽ̨DE�۾���Ȼ������E�����������³�����A��������ʱ��A��������������ֱ�ӵ���C������֪��AC��BC��C��DE��BC��BC=110�ף�DE=9�ף�BD=60�ף���=32�㣬��=68�㣬��AC�ĸ߶ȣ����ο����ݣ�sin32���0.53��cos32���0.85��tan32���0.62��sin68���0.93��cos68���0.37��tan68���2.48��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com