
【题目】如图,抛物线y=a(x﹣m)2+2m﹣2(其中m>1)顶点为P,与y轴相交于点A(0,m﹣1).连接并延长PA、PO分别与x轴、抛物线交于点B、C,连接BC,将△PBC绕点P逆时针旋转得△PB′C′,使点C′正好落在抛物线上.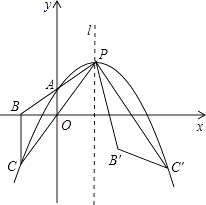
(1)该抛物线的解析式为(用含m的式子表示);
(2)求证:BC∥y轴;
(3)若点B′恰好落在线段BC′上,求此时m的值.
【答案】
(1)y= ![]() (x﹣m)2+2m﹣2
(x﹣m)2+2m﹣2
(2)
证明:如图1,
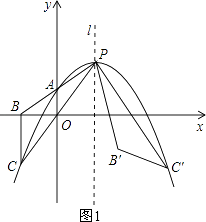
设直线PA的解析式为y=kx+b,
∵点P(m,2m﹣2),点A(0,m﹣1).
∴ ![]() .
.
解得:  .
.
∴直线PA的解析式是y= ![]() x+m﹣1.
x+m﹣1.
当y=0时, ![]() x+m﹣1=0.
x+m﹣1=0.
∵m>1,
∴x=﹣m.
∴点B的横坐标是﹣m.
设直线OP的解析式为y=k′x,
∵点P的坐标为(m,2m﹣2),
∴k′m=2m﹣2.
∴k′= ![]() .
.
∴直线OP的解析式是y= ![]() x.
x.
联立 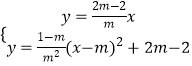
解得: ![]() 或
或 ![]() .
.
∵点C在第三象限,且m>1,
∴点C的横坐标是﹣m.
∴BC∥y轴
(3)
方法一:
解:若点B′恰好落在线段BC′上,
设对称轴l与x轴的交点为D,连接CC′,如图2,
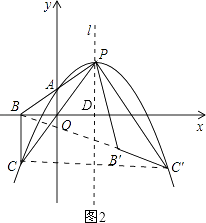
则有∠PB′C′+∠PB′B=180°.
∵△PB′C′是由△PBC绕点P逆时针旋转所得,
∴∠PBC=∠PB′C′,PB=PB′,∠BPB′=∠CPC′.
∴∠PBC+∠PB'B=180°.
∵BC∥AO,
∴∠ABC+∠BAO=180°.
∴∠PB′B=∠BAO.
∵PB=PB′,PC=PC′,
∴∠PB′B=∠PBB′= ![]() ,
,
∴∠PCC′=∠PC′C= ![]() .
.
∴∠PB′B=∠PCC′.
∴∠BAO=∠PCC′.
∵点C关于直线l的对称点为C′,
∴CC′⊥l.
∵OD⊥l,
∴OD∥CC′.
∴∠POD=∠PCC′.
∴∠POD=∠BAO.
∵∠AOB=∠ODP=90°,∠POD=∠BAO,
∴△BAO∽△POD.
∴ ![]() .
.
∵BO=m,PD=2m﹣2,AO=m﹣1,OD=m,
∴ ![]() .
.
解得:m1=2+ ![]() ,m2=2﹣
,m2=2﹣ ![]() .
.
经检验:m1=2+ ![]() ,m2=2﹣
,m2=2﹣ ![]() 都是分式方程的解.
都是分式方程的解.
∵m>1,
∴m=2+ ![]() .
.
∴若点B′恰好落在线段BC′上,此时m的值为2+ ![]() .
.
方法二:
∵点C关于直线l的对称点为C″,
∴Px= ![]() ,
,
∵C(﹣m,2﹣2m),P(m,2m﹣2),
∴m= ![]() ,
,
∴C′X=3m,
∴C′(3m,2﹣2m),
∵将△PBC绕点P逆时针旋转,
∴△BCP≌△B′C′P,
∵点B′恰好落在线段BC′上,
∴线段BP所对的∠BCP=∠B′C′P,
∴点P,B,C,C′四点共圆,(同侧共底的两个三角形顶角相等,则四点共圆)
∵CY=C′Y=2﹣2m,
∴CC′⊥BC,
∴BC′为P,B,C,C′四点共圆所在圆的直径,
∴BP⊥C′P,
∴KBP×KC′P=﹣1,
∵P(m,2m﹣2),
∴C′(3m,2﹣2m),B(﹣m,0),
∴ ![]() =﹣1,
=﹣1,
∴m2﹣4m+2=0,
∴m1=2﹣ ![]() ,m2=2+
,m2=2+ ![]() ,
,
∵m>1,
∴m=2+ ![]() .
.
【解析】(1)解:∵A(0,m﹣1)在抛物线y=a(x﹣m)2+2m﹣2上,
∴a(0﹣m)2+2m﹣2=m﹣1.
∴a= ![]() .
.
∴抛物线的解析式为y= ![]() (x﹣m)2+2m﹣2.
(x﹣m)2+2m﹣2.
所以答案是:y= ![]() (x﹣m)2+2m﹣2.
(x﹣m)2+2m﹣2.


科目:初中数学 来源: 题型:
【题目】以下是某手机店1~4月份的统计图,分析统计图,对3、4月份三星手机的销售情况四个同学得出的以下四个结论,其中正确的为( ) 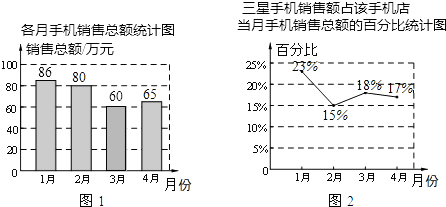
A.4月份三星手机销售额为65万元
B.4月份三星手机销售额比3月份有所上升
C.4月份三星手机销售额比3月份有所下降
D.3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位射击运动员在10次射击训练中,命中靶的环数如图.
请你根据图表,完成下列问题:
(1)
射击序次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩/环 | 8 | 10 | 7 | 9 | 10 | 7 | 10 |
(2)求该运动员这10次射击训练的平均成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD,下列结论中正确的有(填上所有正确结论的序号) ①GH∥DC;
②EG∥AD;
③EH=FG;
④当∠ABC与∠DCB互余时,四边形EFGH是正方形.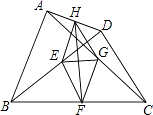
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,设AB=c,BC=a,AC=b,中线AE,BF相交于G,若AE⊥BF.
(1)①当∠ABF=60°,c=4时,求a与b的值;
②当∠ABF=30°,c=2 ![]() 时,a= , b=;
时,a= , b=;
(2)由(1)获得启示,猜想a2 , b2 , c2三者之间满足数量关系式是;(直接写出结果)
(3)如图2,在平行四边形ABCD中,AB=4 ![]() ,BC=3
,BC=3 ![]() ,点E,F,G分别是AD,AB,CD的中点,CF与BG交于P点,若EF⊥FC.利用(2)中的结论,求BG的长.
,点E,F,G分别是AD,AB,CD的中点,CF与BG交于P点,若EF⊥FC.利用(2)中的结论,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() (x2﹣7x+6)的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(x2﹣7x+6)的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(1)用配方法将抛物线的解析式化为顶点式:y=a(x﹣h)2+k(a≠0),并指出顶点M的坐标;
(2)在抛物线的对称轴上找点R,使得CR+AR的值最小,并求出其最小值和点R的坐标;
(3)以AB为直径作⊙N交抛物线于点P(点P在对称轴的左侧),求证:直线MP是⊙N的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
乙校成绩统计表
分数(分) | 人数(人) |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
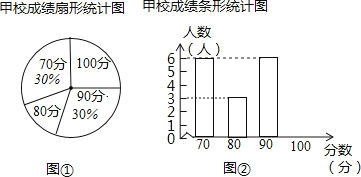
(1)在图①中,“80分”所在扇形的圆心角度数为 ;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com