
【题目】如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD,下列结论中正确的有(填上所有正确结论的序号) ①GH∥DC;
②EG∥AD;
③EH=FG;
④当∠ABC与∠DCB互余时,四边形EFGH是正方形.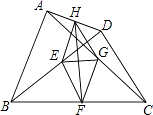
【答案】①③④
【解析】解: 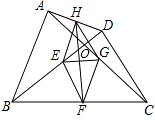
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴EH= ![]() AB,FG=
AB,FG= ![]() AB,GH=
AB,GH= ![]() DC,EF=
DC,EF= ![]() DC,GH∥DC,
DC,GH∥DC,
∵AB=CD,
∴EH=FG=GH=EF,
∴四边形EFGH是菱形,
所以选项①③正确;
当∠ABC与∠DCB互余时,则∠GFC与∠EFB互余,EF⊥FG,四边形EFGH是正方形,所以④正确;
若BC∥AD,设AC与BD交于O,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴AD∥EG,
但BC与AD未必平行,故②不正确.
所以答案是:①③④.
【考点精析】认真审题,首先需要了解正方形的判定方法(先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角),还要掌握平行线分线段成比例(三条平行线截两条直线,所得的对应线段成比例)的相关知识才是答题的关键.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y= ![]() (>0)的图象上任意一点,AB∥x轴交反比例函数y=﹣
(>0)的图象上任意一点,AB∥x轴交反比例函数y=﹣ ![]() 的图象于点B,以AB为边作平行四边形ABCD,其中C,D在x轴上,则平行四边形ABCD的面积为( )
的图象于点B,以AB为边作平行四边形ABCD,其中C,D在x轴上,则平行四边形ABCD的面积为( ) 
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. 
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系中任意两点P1(x1 , y1)、P2(x2 , y2),称|x1﹣x2|+|y1﹣y2|为P1、P2两点的直角距离,记作:d(P1 , P2).P0(2,﹣3)是一定点,Q(x,y)是直线y=kx+b上的一动点,称d(P0 , Q)的最小值为P0到直线y=kx+b的直角距离.若P(a,﹣3)到直线y=x+1的直角距离为6,则a= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=a(x﹣m)2+2m﹣2(其中m>1)顶点为P,与y轴相交于点A(0,m﹣1).连接并延长PA、PO分别与x轴、抛物线交于点B、C,连接BC,将△PBC绕点P逆时针旋转得△PB′C′,使点C′正好落在抛物线上.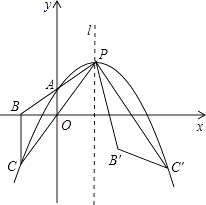
(1)该抛物线的解析式为(用含m的式子表示);
(2)求证:BC∥y轴;
(3)若点B′恰好落在线段BC′上,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在刚刚闭幕的2016全国“两会”,民生话题依然是社会焦点,某市记者为了了解百姓对“两会民生话题”的聚焦点,随机调查了部分市民,并对调查结果进行整理.绘制了如图所示的统计图表(不完整). 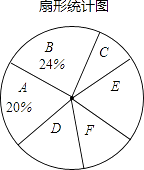
頻数分布表
组别 | 焦点话题 | 频数(人数) |
A | 医疗卫生 | 100 |
B | 食品安全 | m |
C | 教育住房 | 40 |
D | 社会保障 | 80 |
E | 生态环境 | n |
F | 其他 | 60 |
请根据图表中提供的信息解答下列问题:
(1)填空:m= , n= . 扇形统计图中E组,F组所占的百分比分别为、
(2)该市现有人口大约800万,请你估计其中关注B组话题的人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注A组话题的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC绕着点B顺时针旋转90°后得到△A2BC2 , 请在图中画出△A2BC2 , 并求出线段BC旋转过程中所扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知购买1个足球和1个篮球共需130元,购买2个足球和1个篮球共需180元.
(1)求每个足球和每个篮球的售价;
(2)如果某校计划购买这两种球共54个,总费用不超过4000元,问最多可买多少个篮球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com