
【题目】如图,已知抛物线y=![]() (x2﹣7x+6)的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(x2﹣7x+6)的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(1)用配方法将抛物线的解析式化为顶点式:y=a(x﹣h)2+k(a≠0),并指出顶点M的坐标;
(2)在抛物线的对称轴上找点R,使得CR+AR的值最小,并求出其最小值和点R的坐标;
(3)以AB为直径作⊙N交抛物线于点P(点P在对称轴的左侧),求证:直线MP是⊙N的切线.
【答案】
(1)
【解答】解:∵y=![]() (x2﹣7x+6)=
(x2﹣7x+6)=![]() (x2﹣7x)﹣3=
(x2﹣7x)﹣3=![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴抛物线的解析式化为顶点式为:y=![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
顶点M的坐标是(![]() ,
,![]() );
);
(2)
解:∵y=![]() (x2﹣7x+6),
(x2﹣7x+6),
∴当y=0时,![]() (x2﹣7x+6)=0,
(x2﹣7x+6)=0,
解得x=1或6,
∴A(1,0),B(6,0),
∵x=0时,y=﹣3,
∴C(0,﹣3).
连接BC,则BC与对称轴x=![]() 的交点为R,连接AR,
的交点为R,连接AR,
则CR+AR=CR+BR=BC,根据两点之间线段最短可知此时CR+AR的值最小,
最小值为BC=![]() =
=![]() .
.
设直线BC的解析式为y=kx+b,
∵B(6,0),C(0,﹣3),
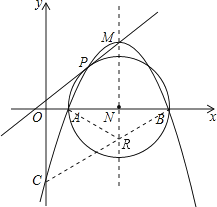
∴![]() ,
,
解得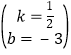 ,
,
∴直线BC的解析式为:y=![]() x﹣3,
x﹣3,
令x=![]() ,得y=
,得y=![]() ×
×![]() ﹣3=
﹣3=![]() ,
,
∴R点坐标为(![]() ,
,![]() );
);
(3)
证明:设点P坐标为(x,![]() x2+
x2+![]() x﹣3).
x﹣3).
∵A(1,0),B(6,0),
∴N(![]() ,0),
,0),
∴以AB为直径的⊙N的半径为![]() AB=
AB=![]() ,
,
∴NP=![]() ,
,
即(x﹣![]() )2+(
)2+(![]() x2+
x2+![]() x﹣3)2=(
x﹣3)2=(![]() )2,
)2,
化简整理得,x4﹣14x3+65x2﹣112x+60=0,
(x﹣1)(x﹣2)(x﹣5)(x﹣6)=0,
解得x1=1(与A重合,舍去),x2=2,x3=5(在对称轴的右侧,舍去),x4=6(与B重合,舍去),
∴点P坐标为(2,2).
∵M(![]() ,
,![]() ),N(
),N(![]() ,0),
,0),
∴PM2=(2﹣![]() )2+(2﹣
)2+(2﹣![]() )2=
)2=![]() ,
,
PN2=(2﹣![]() )2+22=
)2+22=![]() =
=![]() ,
,
MN2=(![]() )2=
)2=![]() ,
,
∴PM2+PN2=MN2,
∴∠MPN=90°,
∵点P在⊙N上,
∴直线MP是⊙N的切线.
【解析】(1)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,即可把一般式转化为顶点式,然后根据二次函数的性质求出抛物线的顶点坐标;
(2)连接BC,则BC与对称轴的交点为R,此时CR+AR的值最小;先求出点A、B、C的坐标,再利用待定系数法求出直线BC的解析式,进而求出其最小值和点R的坐标;
(3)设点P坐标为(x,﹣![]() x2+
x2+![]() x﹣3).根据NP=
x﹣3).根据NP=![]() AB=
AB=![]() 列出方程(x﹣
列出方程(x﹣![]() )2+(﹣
)2+(﹣![]() x2+
x2+![]() x﹣3)2=(
x﹣3)2=(![]() )2 , 解方程得到点P坐标,再计算得出PM2+PN2=MN2 , 根据勾股定理的逆定理得出∠MPN=90°,然后利用切线的判定定理即可证明直线MP是⊙N的切线.
)2 , 解方程得到点P坐标,再计算得出PM2+PN2=MN2 , 根据勾股定理的逆定理得出∠MPN=90°,然后利用切线的判定定理即可证明直线MP是⊙N的切线.


科目:初中数学 来源: 题型:
【题目】已知点A、B、C是直径为6cm的⊙O上的点,且AB=3cm,AC=3 ![]() cm,则∠BAC的度数为( )
cm,则∠BAC的度数为( )
A.15°
B.75°或15°
C.105°或15°
D.75°或105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=a(x﹣m)2+2m﹣2(其中m>1)顶点为P,与y轴相交于点A(0,m﹣1).连接并延长PA、PO分别与x轴、抛物线交于点B、C,连接BC,将△PBC绕点P逆时针旋转得△PB′C′,使点C′正好落在抛物线上.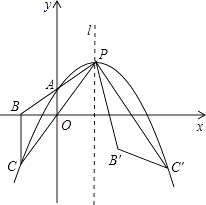
(1)该抛物线的解析式为(用含m的式子表示);
(2)求证:BC∥y轴;
(3)若点B′恰好落在线段BC′上,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC绕着点B顺时针旋转90°后得到△A2BC2 , 请在图中画出△A2BC2 , 并求出线段BC旋转过程中所扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE=![]() GE; ②△AGE≌△ECF; ③∠FCD=45°; ④△GBE∽△ECH,其中,正确的结论有( )
GE; ②△AGE≌△ECF; ③∠FCD=45°; ④△GBE∽△ECH,其中,正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知购买1个足球和1个篮球共需130元,购买2个足球和1个篮球共需180元.
(1)求每个足球和每个篮球的售价;
(2)如果某校计划购买这两种球共54个,总费用不超过4000元,问最多可买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为![]() 米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
(1)求测速点M到该公路的距离;
(2)通过计算判断此车是否超速.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市团委在2015年3月初组成了300个学雷锋小组,现从中随机抽取6个小组在3月份做好事件数的统计情况如图所示:
(1)这6个学雷锋小组在2015年3月份共做好事多少件?
(2)补全条形统计图;
(3)请估计该市300个学雷锋小组在2015年3月份共做好事多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3的对称轴是直线x=1.
(1)求证:2a+b=0
(2)若关于x的方程ax2+bx﹣8=0的一个根为4,求方程的另一个根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com