
【题目】如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.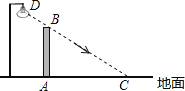
(1)求墙AB的高度(结果精确到0.1米);(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)
(2)如果要缩短影子AC的长度,同时不能改变墙的高度和位置,请你写出两种不同的方法
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,CO⊥AB于O,D在⊙O上,连接BD,CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.
(1)求证:FD是⊙O的切线;
(2)若AF=8,tan∠BDF=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O为△ABC的外接圆,圆心O在AB上. SA'>”不对,理由为:根据规则:每一题抢答对得10分,抢答错扣20分,抢答不到不得分也不扣分.
(1)在图1中,用尺规作图作∠BAC的平分线AD交⊙O于D(保留作图痕迹,不写作法与证明);
(2)如图2,设∠BAC的平分线AD交BC于E,⊙O半径为5,AC=4,连接OD交BC于F.①求证:OD⊥BC;②求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
(1)(1)求EG:BG的值;
(2)(2)求证:AG=OG;
(3)(3)设AG=a,GH=b,HO=c,求a:b:c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列函数(其中n为常数,且n>1)
① y=![]() (x>0); ② y=(n﹣1)x; ③ y=
(x>0); ② y=(n﹣1)x; ③ y=![]() (x>0); ④ y=(1﹣n)x+1; ⑤ y=﹣x2+2nx(x<0)中,y 的值随 x 的值增大而增大的函数有 个.
(x>0); ④ y=(1﹣n)x+1; ⑤ y=﹣x2+2nx(x<0)中,y 的值随 x 的值增大而增大的函数有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC切⊙O于点B,OC平行于弦AD,过点D作DE⊥AB于点E,连结AC,与DE交于点P.求证: 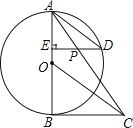
(1)PE=PD
(2)ACPD=APBC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中.顶点为(﹣4,﹣1)的抛物线交y轴于点A(0,3),交x轴于B,C两点.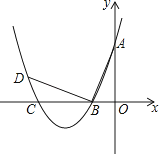
(1)求此抛物线的解析式;
(2)已知点P是抛物线上位于B,C两点之间的一个动点,问:当点P运动到什么位置时,四边形ABPC的面积最大?并求出此时四边形ABPC的面积.
(3)过点B作AB的垂线交抛物线于点D,是否存在以点C为圆心且与线段BD和抛物线的对称轴l同时相切的圆?若存在,求出圆的半径;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
抛物线y=![]() x2上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.
x2上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.
问题解决
如图,在平面直角坐标系中,直线y=kx+1与y轴交于C点,与函数y=![]() x2的图象交于A,B两点,分别过A,B两点作直线y=﹣1的垂线,交于E,F两点.
x2的图象交于A,B两点,分别过A,B两点作直线y=﹣1的垂线,交于E,F两点.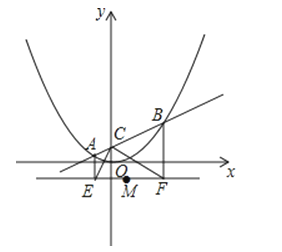
(1)写出点C的坐标,并说明∠ECF=90°
(2)在△PEF中,M为EF中点,P为动点.
①求证:PE2+PF2=2(PM2+EM2);
②已知PE=PF=3,以EF为一条对角线作平行四边形CEDF,若1<PD<2,试求CP的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com