
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道![]() 上确定点D,使CD与
上确定点D,使CD与![]() 垂直,测得CD的长等于21米,在
垂直,测得CD的长等于21米,在![]() 上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
(1)求AB的长(精确到0.1米,参考数据:![]() );
);
(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.
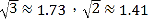
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】进价为每件40元的某商品,售价为每件50元时,每星期可卖出500件,市场调查反映:如果每件的售价每降价1元,每星期可多卖出100件,但售价不能低于每件42元,且每星期至少要销售800件.设每件降价x元 (x为正整数),每星期的利润为y元.
(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)若某星期的利润为5600元,此利润是否是该星期的最大利润?说明理由.
(3)直接写出售价为多少时,每星期的利润不低于5000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题)
在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在直线
在直线![]() 上(
上(![]() 除外),分别经过点
除外),分别经过点![]() 和点
和点![]() 作
作![]() 和
和![]() 的垂线,两条垂线交于点
的垂线,两条垂线交于点![]() ,研究
,研究![]() 和
和![]() 的数量关系.
的数量关系.
(探究发现)
某数学兴趣小组在探究![]() ,
,![]() 的关系时,运用“从特殊到一般”的数学思想,他们发现当点
的关系时,运用“从特殊到一般”的数学思想,他们发现当点![]() 是
是![]() 中点时,只需要取
中点时,只需要取![]() 边的中点
边的中点![]() (如图1),通过推理证明就可以得到
(如图1),通过推理证明就可以得到![]() 和
和![]() 的数量关系,请你按照这种思路直接写出
的数量关系,请你按照这种思路直接写出![]() 和
和![]() 的数量关系;
的数量关系;
(数学思考)
那么点![]() 在直线
在直线![]() 上(
上(![]() 除外)(其他条件不变),上面得到的结论是否仍然成立呢?
除外)(其他条件不变),上面得到的结论是否仍然成立呢?
请你从“点![]() 在线段
在线段![]() 上”“点
上”“点![]() 在线段
在线段![]() 的延长线上”“点
的延长线上”“点![]() 在线段
在线段![]() 的反向延长线上”三种情况中,任选一种情况,在图2中画出图形,并证明你的结论.
的反向延长线上”三种情况中,任选一种情况,在图2中画出图形,并证明你的结论.
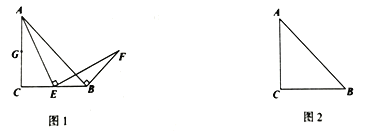
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() ,
,![]() 是线段
是线段![]() 上任意一点(不与点
上任意一点(不与点![]() 、
、![]() 重合),分别以
重合),分别以![]() 、
、![]() 为边,在
为边,在![]() 的同侧作等边
的同侧作等边![]() 和
和![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
![]() 当
当![]() 时,试求
时,试求![]() 的正切值;
的正切值;
![]() 若线段
若线段![]() 是线段
是线段![]() 和
和![]() 的比例中项,试求这时
的比例中项,试求这时![]() 的值;
的值;
![]() 记四边形
记四边形![]() 的面积为
的面积为![]() ,当
,当![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 与
与![]() 是否成正比例,若成正比例,试求出比例系数;若不成正比例,试说明理由.
是否成正比例,若成正比例,试求出比例系数;若不成正比例,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,安全快捷、平稳舒适的中国高铁,为世界高速铁路商业运营树立了新的标杆.随着中国特色社会主义进入新时代,作为“中国名片”的高速铁路也将踏上自己的新征程,跑出发展新速度,这就意味着今后外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从A地到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:
(1)普通列车的行驶路程为多少千米?
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形ABCD的四个角向内折起,恰好拼成一个既无缝隙又无重叠的四边形EFGH,若EH=3,EF=4,那么线段AD与AB的比等于( )
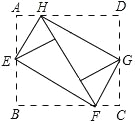
A. 25:24 B. 16:15 C. 5:4 D. 4:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二元一次方程![]() ,通过列举将方程的解写成下列表格的形式:
,通过列举将方程的解写成下列表格的形式:
| -1 |
|
| 5 | 6 |
| 6 | 5 |
| 0 |
|
如果将二元一次方程的解所包含的未知数![]() 的值对应直角坐标系中一个点的横坐标,未知数
的值对应直角坐标系中一个点的横坐标,未知数![]() 的值对应这个点的纵坐标,这样每一个二元一次方程的解,就可以对应直角坐标系中的一个点,例如:方程
的值对应这个点的纵坐标,这样每一个二元一次方程的解,就可以对应直角坐标系中的一个点,例如:方程![]() 的解
的解![]() 的对应点是
的对应点是![]() .
.
(1)表格中的![]() ________,
________,![]() ___________;
___________;
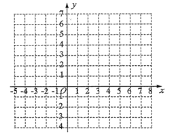
(2)通过以上确定对应点坐标的方法,将表格中给出的五个解依次转化为对应点的坐标,并在所给的直角坐标系中画出这五个点;根据这些点猜想方程![]() 的解的对应点所组成的图形是_________,并写出它的两个特征①__________,②_____________;
的解的对应点所组成的图形是_________,并写出它的两个特征①__________,②_____________;
(3)若点![]() 好落在
好落在![]() 的解对应的点组成的图形上,求
的解对应的点组成的图形上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com