
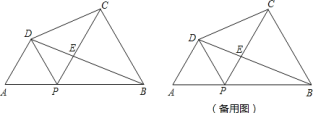
【题目】如图,已知线段![]() ,
,![]() 是线段
是线段![]() 上任意一点(不与点
上任意一点(不与点![]() 、
、![]() 重合),分别以
重合),分别以![]() 、
、![]() 为边,在
为边,在![]() 的同侧作等边
的同侧作等边![]() 和
和![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
![]() 当
当![]() 时,试求
时,试求![]() 的正切值;
的正切值;
![]() 若线段
若线段![]() 是线段
是线段![]() 和
和![]() 的比例中项,试求这时
的比例中项,试求这时![]() 的值;
的值;
![]() 记四边形
记四边形![]() 的面积为
的面积为![]() ,当
,当![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 与
与![]() 是否成正比例,若成正比例,试求出比例系数;若不成正比例,试说明理由.
是否成正比例,若成正比例,试求出比例系数;若不成正比例,试说明理由.
科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④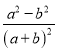 . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);
(2)若![]() 为正整数,且
为正整数,且![]() 为“和谐分式”,请写出
为“和谐分式”,请写出![]() 的值;
的值;
(3)在化简![]() 时,
时,
小东和小强分别进行了如下三步变形:
小东: ![]()
![]()

小强: ![]()
![]()
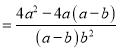
显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
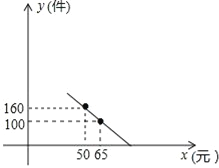
【题目】某商场老板对一种新上市商品的销售情况进行记录,已知这种商品进价为每件40元,经过记录分析发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.
(1)求y与x的函数关系式.
(2)设商场老板每月获得的利润为P(元),求P与x之间的函数关系式;
(3)如果想要每月获得2400元的利润,那么销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论:
①只有一对相似三角形
②EF:ED=1:2
③S1:S2:S3:S4=1:2:4:5
其中正确的结论是( )
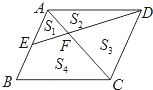
A.①③ B.③ C.① D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩(得分数取正
整数,满分为![]() 分)进行统计,已知
分)进行统计,已知![]() 组的频数
组的频数![]() 比
比![]() 组的频数
组的频数![]() 小,绘制统计频数分别直方图(未完成)
小,绘制统计频数分别直方图(未完成)
和扇形统计图如下,
请解答下列问题:
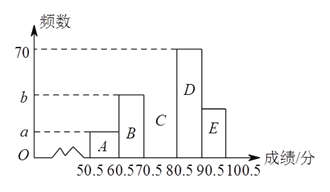
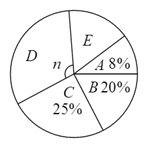
(![]() )样本容量为:__________,
)样本容量为:__________, ![]() 为__________.
为__________.
(![]() )
)![]() 为__________,
为__________, ![]() 组所占比例为__________
组所占比例为__________![]() .
.
(![]() )补全频数分布直方图.
)补全频数分布直方图.
(![]() )若成绩在
)若成绩在![]() 分以上记作优秀,全校共有
分以上记作优秀,全校共有![]() 名学生,估计成绩优秀学生有__________名.
名学生,估计成绩优秀学生有__________名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道![]() 上确定点D,使CD与
上确定点D,使CD与![]() 垂直,测得CD的长等于21米,在
垂直,测得CD的长等于21米,在![]() 上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
(1)求AB的长(精确到0.1米,参考数据:![]() );
);
(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.
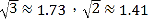
查看答案和解析>>
科目:初中数学 来源: 题型:
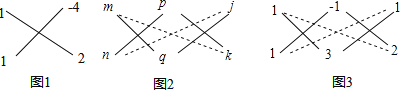
【题目】“十字相乘法”能把二次三项式分解因式,对于形如ax2+bxy+cy2的关于x,y的二次三项式来说,方法的关键是把x2项系数a分解成两个因数a1,a2的积,即a=a1a2,把y2项系数c分解成两个因数c1,c2的积,即c=c1c2,并使a1c2+a2c1正好等于xy项的系数b,那么可以直接写成结果:ax2+bxy+cy2=(a1x+c1y)(a2x+c2y).
例:分解因式:x2﹣2xy﹣8y2.
解:如图1,其中1=1×1,﹣8=(﹣4)×2,而﹣2=1×2+1×(﹣4).
∴x2﹣2xy﹣8y2=(x﹣4y)(x+2y)
而对于形如ax2+bxy+cy2+dx+ey+f的x,y的二元二次式也可以用十字相乘法来分解,如图2,将a分解成mn乘积作为一列,c分解成pq乘积作为第二列,f分解成jk乘积作为第三列,如果mq+np=b,pk+qj=e,mk+nj=d,即第1,2列、第2,3列和第1,3列都满足十字相乘规则,则原式=(mx+py+j)(nx+qy+k);
例:分解因式:x2+2xy﹣3y2+3x+y+2
解:如图3,其中1=1×1,﹣3=(﹣1)×3,2=1×2;
而2=1×3+1×(﹣1),1=(﹣1)×2+3×1,3=1×2+1×1;
∴x2+2xy﹣3y2+3x+y+2=(x﹣y+1)(x+3y+2)
请同学们通过阅读上述材料,完成下列问题:
(1)分解因式:
①6x2﹣17xy+12y2=
②2x2﹣xy﹣6y2+2x+17y﹣12=
③x2﹣xy﹣6y2+2x﹣6y=
(2)若关于x,y的二元二次式x2+7xy﹣18y2﹣5x+my﹣24可以分解成两个一次因式的积,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们学过的分解因式的方法有提取公因式法、公式法及十字相乘法,但有很多的多项式只用上述方法就无法分解,如![]() ,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了.过程为:
,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了.过程为: ![]() ;这种分解因式的方法叫分组分解法.利用这种方法解决下列问题:
;这种分解因式的方法叫分组分解法.利用这种方法解决下列问题:
(1)分解因式:![]()
(2)![]() 三边
三边![]() ,
,![]() ,
,![]() 满足
满足![]() ,判断
,判断![]() 的形状.
的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com