
【题目】“十字相乘法”能把二次三项式分解因式,对于形如ax2+bxy+cy2的关于x,y的二次三项式来说,方法的关键是把x2项系数a分解成两个因数a1,a2的积,即a=a1a2,把y2项系数c分解成两个因数c1,c2的积,即c=c1c2,并使a1c2+a2c1正好等于xy项的系数b,那么可以直接写成结果:ax2+bxy+cy2=(a1x+c1y)(a2x+c2y).
例:分解因式:x2﹣2xy﹣8y2.
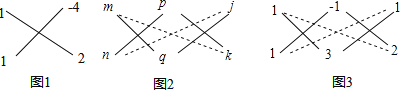
解:如图1,其中1=1×1,﹣8=(﹣4)×2,而﹣2=1×2+1×(﹣4).
∴x2﹣2xy﹣8y2=(x﹣4y)(x+2y)
而对于形如ax2+bxy+cy2+dx+ey+f的x,y的二元二次式也可以用十字相乘法来分解,如图2,将a分解成mn乘积作为一列,c分解成pq乘积作为第二列,f分解成jk乘积作为第三列,如果mq+np=b,pk+qj=e,mk+nj=d,即第1,2列、第2,3列和第1,3列都满足十字相乘规则,则原式=(mx+py+j)(nx+qy+k);
例:分解因式:x2+2xy﹣3y2+3x+y+2
解:如图3,其中1=1×1,﹣3=(﹣1)×3,2=1×2;
而2=1×3+1×(﹣1),1=(﹣1)×2+3×1,3=1×2+1×1;
∴x2+2xy﹣3y2+3x+y+2=(x﹣y+1)(x+3y+2)
请同学们通过阅读上述材料,完成下列问题:
(1)分解因式:
①6x2﹣17xy+12y2=
②2x2﹣xy﹣6y2+2x+17y﹣12=
③x2﹣xy﹣6y2+2x﹣6y=
(2)若关于x,y的二元二次式x2+7xy﹣18y2﹣5x+my﹣24可以分解成两个一次因式的积,求m的值.
科目:初中数学 来源: 题型:
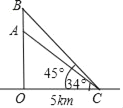
【题目】如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.求AC和AB的长(结果保留小数点后一位)(参考数据:sin34°≈0.56;cos34°≈0.83;tan34°≈0.67)
查看答案和解析>>
科目:初中数学 来源: 题型:
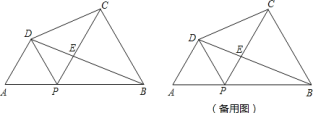
【题目】如图,已知线段![]() ,
,![]() 是线段
是线段![]() 上任意一点(不与点
上任意一点(不与点![]() 、
、![]() 重合),分别以
重合),分别以![]() 、
、![]() 为边,在
为边,在![]() 的同侧作等边
的同侧作等边![]() 和
和![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
![]() 当
当![]() 时,试求
时,试求![]() 的正切值;
的正切值;
![]() 若线段
若线段![]() 是线段
是线段![]() 和
和![]() 的比例中项,试求这时
的比例中项,试求这时![]() 的值;
的值;
![]() 记四边形
记四边形![]() 的面积为
的面积为![]() ,当
,当![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 与
与![]() 是否成正比例,若成正比例,试求出比例系数;若不成正比例,试说明理由.
是否成正比例,若成正比例,试求出比例系数;若不成正比例,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,安全快捷、平稳舒适的中国高铁,为世界高速铁路商业运营树立了新的标杆.随着中国特色社会主义进入新时代,作为“中国名片”的高速铁路也将踏上自己的新征程,跑出发展新速度,这就意味着今后外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从A地到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:
(1)普通列车的行驶路程为多少千米?
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形ABCD的四个角向内折起,恰好拼成一个既无缝隙又无重叠的四边形EFGH,若EH=3,EF=4,那么线段AD与AB的比等于( )
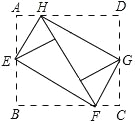
A. 25:24 B. 16:15 C. 5:4 D. 4:3
查看答案和解析>>
科目:初中数学 来源: 题型:
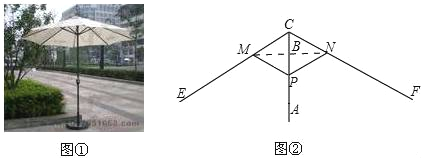
【题目】图1所示的遮阳伞,伞柄垂直于水平地面,其示意图如图2、当伞收紧时,点P与点A重合;当伞慢慢撑开时,动点P由A向B移动;当点P到达点B时,伞张得最开、已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米,CE=CF=18.0分米,BC=2.0分米、设AP=x分米.
(1)求x的取值范围;
(2)若∠CPN=60°,求x的值;
(3)设阳光直射下,伞下的阴影(假定为圆面)面积为y,求y关于x的关系式(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二元一次方程![]() ,通过列举将方程的解写成下列表格的形式:
,通过列举将方程的解写成下列表格的形式:
| -1 |
|
| 5 | 6 |
| 6 | 5 |
| 0 |
|
如果将二元一次方程的解所包含的未知数![]() 的值对应直角坐标系中一个点的横坐标,未知数
的值对应直角坐标系中一个点的横坐标,未知数![]() 的值对应这个点的纵坐标,这样每一个二元一次方程的解,就可以对应直角坐标系中的一个点,例如:方程
的值对应这个点的纵坐标,这样每一个二元一次方程的解,就可以对应直角坐标系中的一个点,例如:方程![]() 的解
的解![]() 的对应点是
的对应点是![]() .
.
(1)表格中的![]() ________,
________,![]() ___________;
___________;
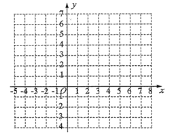
(2)通过以上确定对应点坐标的方法,将表格中给出的五个解依次转化为对应点的坐标,并在所给的直角坐标系中画出这五个点;根据这些点猜想方程![]() 的解的对应点所组成的图形是_________,并写出它的两个特征①__________,②_____________;
的解的对应点所组成的图形是_________,并写出它的两个特征①__________,②_____________;
(3)若点![]() 好落在
好落在![]() 的解对应的点组成的图形上,求
的解对应的点组成的图形上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师出示了如下框中的题目.
已知,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 和点
和点![]() 分别是边
分别是边![]() 和
和![]() 上的点,且始终满足
上的点,且始终满足![]() ,试确定
,试确定![]() 与
与![]() 的大小关系.
的大小关系.

小明与同桌小聪讨论后,进行了如下解答:

(1)(特殊情况,探索结论)如图1,若点![]() 与点
与点![]() 重合时,点
重合时,点![]() 与点
与点![]() 重合,容易得到
重合,容易得到![]() 与
与![]() 的大小关系.请你直接写出结论:
的大小关系.请你直接写出结论:![]() ____________
____________![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”).
”).
(2)(特例启发,解答题目)如图2,若点![]() 不与点
不与点![]() 重合时,
重合时,![]() 与
与![]() 的大小关系是:
的大小关系是:![]() _________
_________![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”).理由如下:连结
”).理由如下:连结![]() ,(请你完成剩下的解答过程)
,(请你完成剩下的解答过程)
(3)(拓展结论,设计新题)在![]() 中
中![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 和点
和点![]() 分别是直线
分别是直线![]() 和直线
和直线![]() 上的点,且始终满足
上的点,且始终满足![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.(请你直接写出结果)
的长.(请你直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
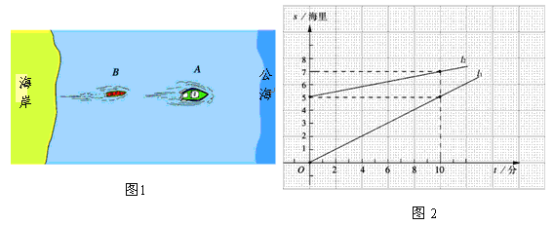
【题目】我国边防局接到情报,近海处有一可疑船只![]() 正向公海方向行驶,边防部迅速派出快艇
正向公海方向行驶,边防部迅速派出快艇![]() 追赶(如图1) .图2中
追赶(如图1) .图2中![]() 分别表示两船相对于海岸的距离
分别表示两船相对于海岸的距离![]() (海里)与追赶时间
(海里)与追赶时间![]() (分)之间的关系.根据图象问答问题:
(分)之间的关系.根据图象问答问题:
(1)①直线![]() 与直线
与直线![]() 中 表示
中 表示![]() 到海岸的距离与追赶时间之间的关系;
到海岸的距离与追赶时间之间的关系;
②![]() 与
与![]() 比较 速度快;
比较 速度快;
③如果一直追下去,那么![]() ________ (填 “能”或“不能")追上
________ (填 “能”或“不能")追上![]() ;
;
④可疑船只![]() 速度是 海里/分,快艇
速度是 海里/分,快艇![]() 的速度是 海里/分;
的速度是 海里/分;
(2)![]() 与
与![]() 对应的两个一次函数表达式
对应的两个一次函数表达式![]() 与
与![]() 中
中![]() 的实际意义各是什么?并直接写出两个具体表达式.
的实际意义各是什么?并直接写出两个具体表达式.
(3)![]() 分钟内
分钟内![]() 能否追上
能否追上![]() ?为什么?
?为什么?
(4)当![]() 逃离海岸
逃离海岸![]() 海里的公海时,
海里的公海时, 将无法对其进行检查,照此速度,
将无法对其进行检查,照此速度,![]() 能否在
能否在![]() 逃入公海前将其拦截?为什么?
逃入公海前将其拦截?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com