
ЁОЬтФПЁПЪ§бЇПЮЩЯЃЌеХРЯЪІГіЪОСЫШчЯТПђжаЕФЬтФПЃЎ
вбжЊЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() КЭЕу
КЭЕу![]() ЗжБ№ЪЧБп
ЗжБ№ЪЧБп![]() КЭ
КЭ![]() ЩЯЕФЕуЃЌЧвЪМжеТњзу
ЩЯЕФЕуЃЌЧвЪМжеТњзу![]() ЃЌЪдШЗЖЈ
ЃЌЪдШЗЖЈ![]() гы
гы![]() ЕФДѓаЁЙиЯЕЃЎ
ЕФДѓаЁЙиЯЕЃЎ

аЁУїгыЭЌзРаЁДЯЬжТлКѓЃЌНјааСЫШчЯТНтД№ЃК

ЃЈ1ЃЉЃЈЬиЪтЧщПіЃЌЬНЫїНсТлЃЉШчЭМ1ЃЌШєЕу![]() гыЕу
гыЕу![]() жиКЯЪБЃЌЕу
жиКЯЪБЃЌЕу![]() гыЕу
гыЕу![]() жиКЯЃЌШнвзЕУЕН
жиКЯЃЌШнвзЕУЕН![]() гы
гы![]() ЕФДѓаЁЙиЯЕЃЎЧыФужБНгаДГіНсТлЃК
ЕФДѓаЁЙиЯЕЃЎЧыФужБНгаДГіНсТлЃК![]() ____________
____________![]() ЃЈЬюЁА
ЃЈЬюЁА![]() ЁБЃЌЁА
ЁБЃЌЁА![]() ЁБЛђЁА
ЁБЛђЁА![]() ЁБЃЉЃЎ
ЁБЃЉЃЎ
ЃЈ2ЃЉЃЈЬиР§ЦєЗЂЃЌНтД№ЬтФПЃЉШчЭМ2ЃЌШєЕу![]() ВЛгыЕу
ВЛгыЕу![]() жиКЯЪБЃЌ
жиКЯЪБЃЌ![]() гы
гы![]() ЕФДѓаЁЙиЯЕЪЧЃК
ЕФДѓаЁЙиЯЕЪЧЃК![]() _________
_________![]() ЃЈЬюЁА
ЃЈЬюЁА![]() ЁБЃЌЁА
ЁБЃЌЁА![]() ЁБЛђЁА
ЁБЛђЁА![]() ЁБЃЉЃЎРэгЩШчЯТЃКСЌНс
ЁБЃЉЃЎРэгЩШчЯТЃКСЌНс![]() ЃЌЃЈЧыФуЭъГЩЪЃЯТЕФНтД№Й§ГЬЃЉ
ЃЌЃЈЧыФуЭъГЩЪЃЯТЕФНтД№Й§ГЬЃЉ
ЃЈ3ЃЉЃЈЭиеЙНсТлЃЌЩшМЦаТЬтЃЉдк![]() жа
жа![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() КЭЕу
КЭЕу![]() ЗжБ№ЪЧжБЯп
ЗжБ№ЪЧжБЯп![]() КЭжБЯп
КЭжБЯп![]() ЩЯЕФЕуЃЌЧвЪМжеТњзу
ЩЯЕФЕуЃЌЧвЪМжеТњзу![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎЃЈЧыФужБНгаДГіНсЙћЃЉ
ЕФГЄЃЎЃЈЧыФужБНгаДГіНсЙћЃЉ
ЁОД№АИЁПЃЈ1ЃЉ=ЃЛЃЈ2ЃЉ=ЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉ1Лђ3
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕШжБНЧШ§НЧаЮаББпЕФжаЯпЕШгкаББпЕФвЛАыНтД№МДПЩЃЛ
ЃЈ2ЃЉСЌНс![]() ЃЌжЄУїЁїBDEЁеЁїADFМДПЩЃЛ
ЃЌжЄУїЁїBDEЁеЁїADFМДПЩЃЛ
ЃЈ3ЃЉЗжЫФжжЧщПіЧѓНтЃКЂйЕБЕуEдкBAЕФбгГЄЯпЩЯЃЌЕуFдкACЕФбгГЄЯпЩЯЃЛЂкЕБЕуEдкABЕФбгГЄЯпЩЯЃЌЕуFдкCAЕФбгГЄЯпЩЯЃЛЂлЕБЕуEдкABЕФбгГЄЯпЩЯЃЌЕуFдкACЕФбгГЄЯпЩЯЃЛЂмЕБЕуEдкBAЕФбгГЄЯпЩЯЃЌЕуFдкCAЕФбгГЄЯпЩЯЃЎ
ЃЈ1ЃЉЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЁЯACD=45Ёу.
Ёп![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
ЁрЁЯCAD=45ЁуЃЌ
ЁрЁЯCAD=ЁЯACDЃЌ
ЁрAD=CDЃЌ
МДDE=DFЃЛ
ЃЈ2ЃЉСЌНс![]() ЃЌ
ЃЌ
Ёп![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
ЁрAD=![]() =BDЃЎ
=BDЃЎ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
ЁрЁЯB=ЁЯC=ЁЯCAD=ЁЯBAD=45ЁуЃЌADЁЭBCЃЌ
ЁрЁЯADE+ЁЯBDE=90ЁуЃЎ
ЁпDEЁЭDFЃЌ
ЁрЁЯADE+ЁЯADF=90ЁуЃЌ
ЁрЁЯBDE=ЁЯADFЃЎ
дкЁїBDEКЭЁїADFжаЃЌ
ЁпЁЯB=ЁЯCAD=45ЁуЃЌ
AD=BDЃЌ
ЁЯBDE=ЁЯADFЃЌ
ЁрЁїBDEЁеЁїADFЃЌ
ЁрDE=DFЃЛ
ЃЈ3ЃЉЂйЕБЕуEдкBAЕФбгГЄЯпЩЯЃЌЕуFдкACЕФбгГЄЯпЩЯЃЌШчЭМ1ЃЌ
гЩЃЈ2ЃЉжЊЃЌAD=CDЃЌЁЯCAD=ЁЯACB=45ЁуЃЌ
ЁрЁЯDAE=ЁЯDCE=135ЁуЃЎ
ЁпDEЁЭDFЃЌEЁЭDFЃЌ
ЁрЁЯCDE+ЁЯCDF=90ЁуЃЌЁЯADE+ЁЯCDE=90ЁуЃЌ
ЁрЁЯCDF=ЁЯADEЃЌ
дкЁїADEКЭЁїCDFжаЃЌ
ЁпЁЯDAE=ЁЯDCEЃЌ
AD=CDЃЌ
ЁЯADE=ЁЯCDFЃЌ
ЁрЁїADEЁеЁїCDFЃЌ
ЁрCF=AEЃЌ
ЁпBE=2ЃЌЃЌAB=1ЃЌ
ЁрCF=AE=2-1=1ЃЛ
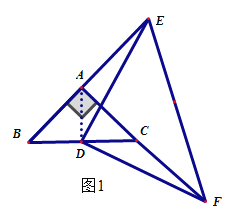
ЂкЕБЕуEдкABЕФбгГЄЯпЩЯЃЌЕуFдкCAЕФбгГЄЯпЩЯЃЌШчЭМ2ЃЌ
гыЂйЭЌРэПЩжЄЁїADFЁеЁїBDEЃЌ
ЁрAF=BE=2ЃЌ
ЁпAC=1ЃЌ
ЁрCF=2+1=3ЃЛ
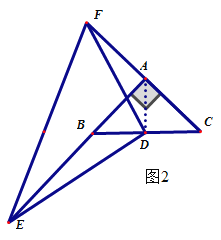
ЂлЕБЕуEдкABЕФбгГЄЯпЩЯЃЌЕуFдкACЕФбгГЄЯпЩЯЃЌШчЭМ3ЃЌ СЌНгADЃЌВЂбгГЄНЛEFгыHЃЌ
ЁпЁЯ5=ЁЯ1+ЁЯ3ЃЌЁЯ6=ЁЯ2+ЁЯ4ЃЌ
ЁрЁЯ5+ЁЯ6=ЁЯ1+ЁЯ3+ЁЯ2+ЁЯ4ЃЌ
ЁпЁЯ1+ЁЯ2=90ЁуЃЌЁЯ5+ЁЯ6=90ЁуЃЌ
ЁрЁЯ3+ЁЯ4=0ЁуЃЌВЛКЯЬтвтЃЌДЫжжЧщПіВЛГЩСЂЃЛ

ЂмЕБЕуEдкBAЕФбгГЄЯпЩЯЃЌЕуFдкCAЕФбгГЄЯпЩЯЃЌШчЭМ4ЃЌ
ЭЌЂлЕФЗНЗЈПЩЫЕУїДЫжжЧщПівВВЛГЩСЂЃЎ
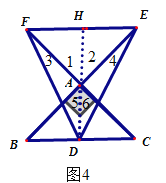
злЩЯПЩжЊЃЌCFЕФГЄЪЧ1Лђ3ЃЎ


 ЦкФЉМЏНсКХЯЕСаД№АИ
ЦкФЉМЏНсКХЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌAB=AC=10cmЃЌBC=8cmЃЌЕуDЮЊABЕФжаЕуЃЎШчЙћЕуPдкЯпЖЮBCЩЯвд3cm/sЕФЫйЖШгЩЕуBЯђCЕудЫЖЏЃЌЭЌЪБЃЌЕуQдкЯпЖЮCAЩЯгЩЕуCЯђAЕудЫЖЏЃЎ

ЃЈ1ЃЉШєЕуQЕФдЫЖЏЫйЖШгыЕуPЕФдЫЖЏЫйЖШЯрЕШЃЌОЙ§1УыКѓЃЌЁїBPDгыЁїCQPЪЧЗёШЋЕШЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ2ЃЉШєЕуQЕФдЫЖЏЫйЖШгыЕуPЕФдЫЖЏЫйЖШВЛЯрЕШЃЌЕБЕуQЕФдЫЖЏЫйЖШЮЊЖрЩйЪБЃЌФмЙЛЪЙЁїBPDгыЁїCQPШЋЕШЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЪЎзжЯрГЫЗЈЁБФмАбЖўДЮШ§ЯюЪНЗжНтвђЪНЃЌЖдгкаЮШчax2+bxy+cy2ЕФЙигкxЃЌyЕФЖўДЮШ§ЯюЪНРДЫЕЃЌЗНЗЈЕФЙиМќЪЧАбx2ЯюЯЕЪ§aЗжНтГЩСНИівђЪ§a1ЃЌa2ЕФЛ§ЃЌМДaЃНa1a2ЃЌАбy2ЯюЯЕЪ§cЗжНтГЩСНИівђЪ§c1ЃЌc2ЕФЛ§ЃЌМДcЃНc1c2ЃЌВЂЪЙa1c2+a2c1е§КУЕШгкxyЯюЕФЯЕЪ§bЃЌФЧУДПЩвджБНгаДГЩНсЙћЃКax2+bxy+cy2ЃНЃЈa1x+c1yЃЉЃЈa2x+c2yЃЉЃЎ
Р§ЃКЗжНтвђЪНЃКx2Љ2xyЉ8y2ЃЎ
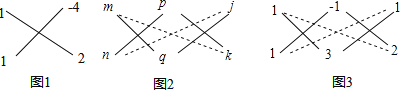
НтЃКШчЭМ1ЃЌЦфжа1ЃН1ЁС1ЃЌЉ8ЃНЃЈЉ4ЃЉЁС2ЃЌЖјЉ2ЃН1ЁС2+1ЁСЃЈЉ4ЃЉЃЎ
Ёрx2Љ2xyЉ8y2ЃНЃЈxЉ4yЃЉЃЈx+2yЃЉ
ЖјЖдгкаЮШчax2+bxy+cy2+dx+ey+fЕФxЃЌyЕФЖўдЊЖўДЮЪНвВПЩвдгУЪЎзжЯрГЫЗЈРДЗжНтЃЌШчЭМ2ЃЌНЋaЗжНтГЩmnГЫЛ§зїЮЊвЛСаЃЌcЗжНтГЩpqГЫЛ§зїЮЊЕкЖўСаЃЌfЗжНтГЩjkГЫЛ§зїЮЊЕкШ§СаЃЌШчЙћmq+npЃНbЃЌpk+qjЃНeЃЌmk+njЃНdЃЌМДЕк1ЃЌ2СаЁЂЕк2ЃЌ3СаКЭЕк1ЃЌ3СаЖМТњзуЪЎзжЯрГЫЙцдђЃЌдђдЪНЃНЃЈmx+py+jЃЉЃЈnx+qy+kЃЉЃЛ
Р§ЃКЗжНтвђЪНЃКx2+2xyЉ3y2+3x+y+2
НтЃКШчЭМ3ЃЌЦфжа1ЃН1ЁС1ЃЌЉ3ЃНЃЈЉ1ЃЉЁС3ЃЌ2ЃН1ЁС2ЃЛ
Жј2ЃН1ЁС3+1ЁСЃЈЉ1ЃЉЃЌ1ЃНЃЈЉ1ЃЉЁС2+3ЁС1ЃЌ3ЃН1ЁС2+1ЁС1ЃЛ
Ёрx2+2xyЉ3y2+3x+y+2ЃНЃЈxЉy+1ЃЉЃЈx+3y+2ЃЉ
ЧыЭЌбЇУЧЭЈЙ§дФЖСЩЯЪіВФСЯЃЌЭъГЩЯТСаЮЪЬтЃК
ЃЈ1ЃЉЗжНтвђЪНЃК
Ђй6x2Љ17xy+12y2ЃНЁЁ ЁЁ
Ђк2x2ЉxyЉ6y2+2x+17yЉ12ЃНЁЁ ЁЁ
Ђлx2ЉxyЉ6y2+2xЉ6yЃНЁЁ ЁЁ
ЃЈ2ЃЉШєЙигкxЃЌyЕФЖўдЊЖўДЮЪНx2+7xyЉ18y2Љ5x+myЉ24ПЩвдЗжНтГЩСНИівЛДЮвђЪНЕФЛ§ЃЌЧѓmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊдкЦНУцжБНЧзјБъЯЕжаЃЌЫФБпаЮABCDЪЧСтаЮЃЌЦфжаBЕузјБъЪЧ(8ЃЌ2)ЃЌDЕузјБъЪЧ(0ЃЌ2)ЃЌЕуAдкxжсЩЯЃЌдђСтаЮABCDЕФжмГЄЪЧЃЈ ЃЉ
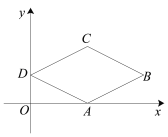
A.2![]()
B.8
C.8![]()
D.12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕчЪгЬЈЕФвЛЕЕгщРжадНкФПжаЃЌдкгЮЯЗPKЛЗНкЃЌЮЊСЫЫцЛњЗжбЁгЮЯЗЫЋЗНЕФзщдБЃЌжїГжШЫЩшМЦСЫвдЯТгЮЯЗЃКгУВЛЭИУїЕФАзВМАќзЁШ§ИљбеЩЋГЄЖЬЯрЭЌЕФЯИЩўAA1ЁЂBB1ЁЂCC1ЃЌжЛТЖГіЫќУЧЕФЭЗКЭЮВЃЈШчЭМЫљЪОЃЉЃЌгЩМзЁЂввСНЮЛМЮБіЗжБ№ДгАзВМСНЖЫИїбЁвЛИљЯИЩўЃЌВЂРГіЃЌШєСНШЫбЁжаЭЌвЛИљЯИЩўЃЌдђСНШЫЭЌЖгЃЌЗёдђЛЅЮЊЗДЗНЖгдБЃЎ
ЃЈ1ЃЉШєМзМЮБіДгжаШЮвтбЁдёвЛИљЯИЩўРГіЃЌЧѓЫћЧЁКУГщГіЯИЩўAA1ЕФИХТЪЃЛ
ЃЈ2ЃЉЧыгУЛЪїзДЭМЗЈЛђСаБэЗЈЃЌЧѓМзЁЂввСНЮЛМЮБіФмЗжЮЊЭЌЖгЕФИХТЪЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌAB=BDЃЌЕуEЁЂFЗжБ№ЪЧABЁЂADЩЯШЮвтЕФЕуЃЈВЛгыЖЫЕужиКЯЃЉЃЌЧвAE=DFЃЌСЌНгBFгыDEЯрНЛгкЕуGЃЌСЌНгCGгыBDЯрНЛгкЕуHЃЎИјГіШчЯТМИИіНсТлЃКЂйЁїAEDЁеЁїDFBЃЛЂкSЫФБпаЮBCDG=![]() ЃЛЂлШєAF=2DFЃЌдђBG=6GFЃЛЂмCGгыBDвЛЖЈВЛДЙжБЃЛЂнЁЯBGEЕФДѓаЁЮЊЖЈжЕЃЎ
ЃЛЂлШєAF=2DFЃЌдђBG=6GFЃЛЂмCGгыBDвЛЖЈВЛДЙжБЃЛЂнЁЯBGEЕФДѓаЁЮЊЖЈжЕЃЎ
Цфжае§ШЗЕФНсТлИіЪ§ЮЊЃЈ ЃЉ

A. 4 B. 3 C. 2 D. 1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧбЇЙ§ЕФЗжНтвђЪНЕФЗНЗЈгаЬсШЁЙЋвђЪНЗЈЁЂЙЋЪНЗЈМАЪЎзжЯрГЫЗЈЃЌЕЋгаКмЖрЕФЖрЯюЪНжЛгУЩЯЪіЗНЗЈОЭЮоЗЈЗжНтЃЌШч![]() ЃЌЮвУЧЯИаФЙлВьетИіЪНзгОЭЛсЗЂЯжЃЌЧАСНЯюЗћКЯЦНЗНВюЙЋЪНЃЌКѓСНЯюПЩЬсШЁЙЋвђЪНЃЌЧАКѓСНВПЗжЗжБ№ЗжНтвђЪНКѓЛсВњЩњЙЋвђЪНЃЌШЛКѓЬсШЁЙЋвђЪНОЭПЩвдЭъГЩећИіЪНзгЕФЗжНтвђЪНСЫЃЎЙ§ГЬЮЊЃК
ЃЌЮвУЧЯИаФЙлВьетИіЪНзгОЭЛсЗЂЯжЃЌЧАСНЯюЗћКЯЦНЗНВюЙЋЪНЃЌКѓСНЯюПЩЬсШЁЙЋвђЪНЃЌЧАКѓСНВПЗжЗжБ№ЗжНтвђЪНКѓЛсВњЩњЙЋвђЪНЃЌШЛКѓЬсШЁЙЋвђЪНОЭПЩвдЭъГЩећИіЪНзгЕФЗжНтвђЪНСЫЃЎЙ§ГЬЮЊЃК ![]() ЃЛетжжЗжНтвђЪНЕФЗНЗЈНаЗжзщЗжНтЗЈЃЎРћгУетжжЗНЗЈНтОіЯТСаЮЪЬтЃК
ЃЛетжжЗжНтвђЪНЕФЗНЗЈНаЗжзщЗжНтЗЈЃЎРћгУетжжЗНЗЈНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉЗжНтвђЪНЃК![]()
ЃЈ2ЃЉ![]() Ш§Бп
Ш§Бп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Тњзу
Тњзу![]() ЃЌХаЖЯ
ЃЌХаЖЯ![]() ЕФаЮзДЃЎ
ЕФаЮзДЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтбЇЩњЕФАВШЋвтЪЖЧщПіЃЌдкШЋаЃЗЖЮЇФкЫцЛњГщШЁВПЗжбЇЩњНјааЮЪОэЕїВщЃЌИљОнЕїВщНсЙћЃЌАббЇЩњЕФАВШЋвтЪЖЗжГЩЁАЕБЁЁБЁЂЁАвЛАуЁБЁЂЁАНЯЧПЁБЁЂ ЁАКмЧПЁБЫФИіВуДЮЃЌВЂЛцжЦГЩШчЯТСНЗљЩаВЛЭъећЕФЭГМЦЭМЃК
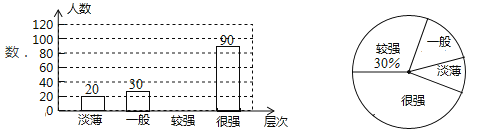
ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉИУаЃга![]() УћбЇЩњЃЌЯжвЊЖдАВШЋвтЪЖЮЊЁАЕБЁЁБЁЂЁАвЛАу"ЕФбЇЩњЧПЛЏАВШЋНЬг§ЃЌИљОнЕїВщНсЙћЃЌЙРМЦШЋаЃашвЊЧПЛЏАВШЋНЬг§ЕФбЇЩњдМгаЖрЩйУћЃП
УћбЇЩњЃЌЯжвЊЖдАВШЋвтЪЖЮЊЁАЕБЁЁБЁЂЁАвЛАу"ЕФбЇЩњЧПЛЏАВШЋНЬг§ЃЌИљОнЕїВщНсЙћЃЌЙРМЦШЋаЃашвЊЧПЛЏАВШЋНЬг§ЕФбЇЩњдМгаЖрЩйУћЃП
ЃЈ2ЃЉЧыНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЎ
ЃЈ3ЃЉЧѓГіАВШЋвтЪЖЮЊЁАНЯЧПЁБЕФбЇЩњЫљеМЕФАйЗжБШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
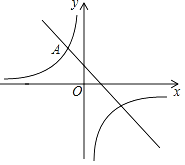
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓгывЛДЮКЏЪ§y=Љx+1ЕФЭМЯѓЕФвЛИіНЛЕуЮЊAЃЈЉ1ЃЌmЃЉЃЎ
ЕФЭМЯѓгывЛДЮКЏЪ§y=Љx+1ЕФЭМЯѓЕФвЛИіНЛЕуЮЊAЃЈЉ1ЃЌmЃЉЃЎ
ЃЈ1ЃЉЧѓетИіЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЙћвЛДЮКЏЪ§y=Љx+1ЕФЭМЯѓгыxжсНЛгкЕуBЃЈnЃЌ0ЃЉЃЌЧыШЗЖЈЕБxЃМnЪБЃЌЖдгІЕФЗДБШР§КЏЪ§y=![]() ЕФжЕЕФЗЖЮЇЃЎ
ЕФжЕЕФЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com