
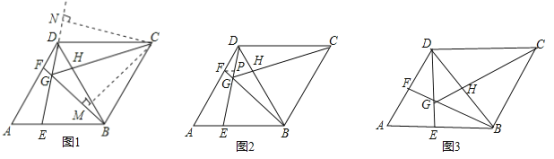
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:①△AED≌△DFB;②S四边形BCDG=![]() ;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.
;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.
其中正确的结论个数为( )

A. 4 B. 3 C. 2 D. 1
【答案】B
【解析】试题分析:①∵ABCD为菱形,∴AB=AD,∵AB=BD,∴△ABD为等边三角形,∴∠A=∠BDF=60°,又∵AE=DF,AD=BD,∴△AED≌△DFB,故本选项正确;
②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,即∠BGD+∠BCD=180°,∴点B、C、D、G四点共圆,∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°,∴∠BGC=∠DGC=60°,过点C作CM⊥GB于M,CN⊥GD于N(如图1),则△CBM≌△CDN(AAS),∴S四边形BCDG=S四边形CMGN,S四边形CMGN=2S△CMG,∵∠CGM=60°,∴GM=![]() CG,CM=
CG,CM=![]() CG,∴S四边形CMGN=2S△CMG=2×
CG,∴S四边形CMGN=2S△CMG=2×![]() ×
×![]() CG×
CG×![]() CG=
CG=![]() ,故本选项错误;
,故本选项错误;
③过点F作FP∥AE于P点(如图2),∵AF=2FD,∴FP:AE=DF:DA=1:3,∵AE=DF,AB=AD,∴BE=2AE,∴FP:BE=FP: ![]() AE=1:6,∵FP∥AE,∴PF∥BE,∴FG:BG=FP:BE=1:6,即BG=6GF,故本选项正确;
AE=1:6,∵FP∥AE,∴PF∥BE,∴FG:BG=FP:BE=1:6,即BG=6GF,故本选项正确;
④当点E,F分别是AB,AD中点时(如图3),由(1)知,△ABD,△BDC为等边三角形,∵点E,F分别是AB,AD中点,∴∠BDE=∠DBG=30°,∴DG=BG,在△GDC与△BGC中,∵DG=BG,CG=CG,CD=CB,∴△GDC≌△BGC,∴∠DCG=∠BCG,∴CH⊥BD,即CG⊥BD,故本选项错误;
⑤∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°,为定值,故本选项正确;
综上所述,正确的结论有①③⑤,共3个,故选B.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
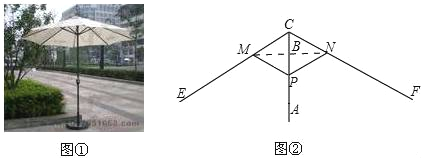
【题目】图1所示的遮阳伞,伞柄垂直于水平地面,其示意图如图2、当伞收紧时,点P与点A重合;当伞慢慢撑开时,动点P由A向B移动;当点P到达点B时,伞张得最开、已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米,CE=CF=18.0分米,BC=2.0分米、设AP=x分米.
(1)求x的取值范围;
(2)若∠CPN=60°,求x的值;
(3)设阳光直射下,伞下的阴影(假定为圆面)面积为y,求y关于x的关系式(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
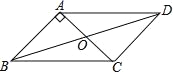
【题目】已知:如图,在ABCD中,对角线AC,BD交于点O,AB⊥AC,AB=1,BC=![]() .
.
(1)求平行四边形ABCD的面积S□ABCD;
(2)求对角线BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师出示了如下框中的题目.
已知,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 和点
和点![]() 分别是边
分别是边![]() 和
和![]() 上的点,且始终满足
上的点,且始终满足![]() ,试确定
,试确定![]() 与
与![]() 的大小关系.
的大小关系.

小明与同桌小聪讨论后,进行了如下解答:

(1)(特殊情况,探索结论)如图1,若点![]() 与点
与点![]() 重合时,点
重合时,点![]() 与点
与点![]() 重合,容易得到
重合,容易得到![]() 与
与![]() 的大小关系.请你直接写出结论:
的大小关系.请你直接写出结论:![]() ____________
____________![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”).
”).
(2)(特例启发,解答题目)如图2,若点![]() 不与点
不与点![]() 重合时,
重合时,![]() 与
与![]() 的大小关系是:
的大小关系是:![]() _________
_________![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”).理由如下:连结
”).理由如下:连结![]() ,(请你完成剩下的解答过程)
,(请你完成剩下的解答过程)
(3)(拓展结论,设计新题)在![]() 中
中![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 和点
和点![]() 分别是直线
分别是直线![]() 和直线
和直线![]() 上的点,且始终满足
上的点,且始终满足![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.(请你直接写出结果)
的长.(请你直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的角平分线.
的角平分线.
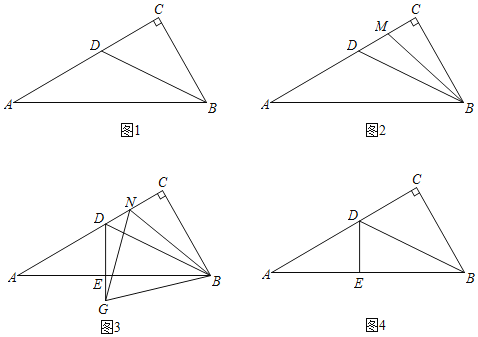
(1)如图 1,求证:![]() ;
;
(2)如图 2,作![]() 的角平分线交线段
的角平分线交线段![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;
(3)如图 3,过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 上一点(不与
上一点(不与 ![]() 重合),以
重合),以![]() 为一边,在
为一边,在![]() 的下方作
的下方作![]() ,
,![]() 交
交![]() 延长线于点
延长线于点![]() ,试探究线段
,试探究线段![]() ,
,![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
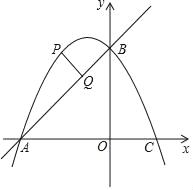
【题目】如图,在平面直角坐标系中,直线y=x+2与坐标轴交于A、B两点,点A在x轴上,点B在y轴上,C点的坐标为(1,0),抛物线y=ax2+bx+c经过点A、B、C.
(1)求该抛物线的解析式;
(2)根据图象直接写出不等式ax2+(b﹣1)x+c>2的解集;
(3)点P是抛物线上一动点,且在直线AB上方,过点P作AB的垂线段,垂足为Q点.当PQ=![]() 时,求P点坐标.
时,求P点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com