
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的角平分线.
的角平分线.
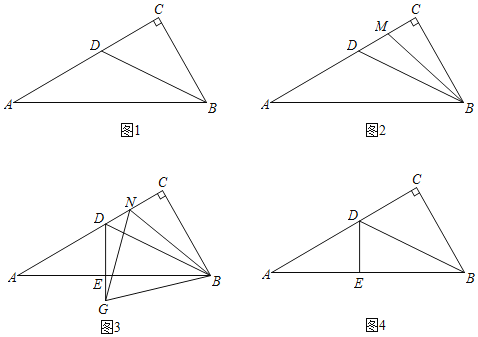
(1)如图 1,求证:![]() ;
;
(2)如图 2,作![]() 的角平分线交线段
的角平分线交线段![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;
(3)如图 3,过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 上一点(不与
上一点(不与 ![]() 重合),以
重合),以![]() 为一边,在
为一边,在![]() 的下方作
的下方作![]() ,
,![]() 交
交![]() 延长线于点
延长线于点![]() ,试探究线段
,试探究线段![]() ,
,![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)见解析;(2)![]() 的面积=
的面积=![]() ;(3)若点
;(3)若点![]() 在
在![]() 上时,
上时,![]() ,理由见解析;若点
,理由见解析;若点![]() 在
在![]() 上时,
上时,![]()
![]() ,理由见解析.
,理由见解析.
【解析】
(1)利用角平分线的性质,证得![]() ,再证得
,再证得![]() ,在
,在![]() 中,利用
中,利用![]() 角所对直角边等于斜边的一半即可证得结论;
角所对直角边等于斜边的一半即可证得结论;
(2)作![]() ,先证得
,先证得![]() ,在
,在![]() 和
和![]() 中,分别利用
中,分别利用![]() 角所对直角边等于斜边的一半求得BC和CD的长,从而求得
角所对直角边等于斜边的一半求得BC和CD的长,从而求得![]() 的长,即可求得
的长,即可求得![]() 的面积;
的面积;
(3)分两种情况讨论,点![]() 在
在![]() 上和点
上和点![]() 在
在![]() 上时,采用补短的方法,利用全等三角形的判定和性质即可证明.
上时,采用补短的方法,利用全等三角形的判定和性质即可证明.
(1)在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的角平分线,
的角平分线,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)如图2,过点![]() 作
作![]() ,
,
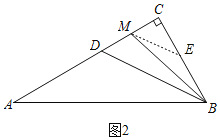
由(1)得![]() ,
,
∵![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() 的面积
的面积![]()
![]() ;
;
(3)若点![]() 在
在![]() 上时,
上时,![]() ,
,
理由如下:如图3所示:延长![]() 使得
使得![]() ,连接
,连接![]() ,
,
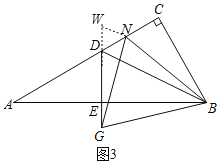
![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() 于点
于点![]() ,
,
![]() ,
,
![]() ,且
,且![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
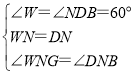 ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)若点![]() 在
在![]() 上时,
上时,![]() ,
,
理由如下:如图4,延长![]() 至
至![]() ,使得
,使得![]() ,连接
,连接![]() ,
,

由(1)得![]() ,
,
∵![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
即![]() ,
,
在![]() 和
和![]() 中,
中,
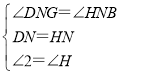 ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于点
轴交于点![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() .
.![]() 为
为![]() 的中点,
的中点,![]() 为射线
为射线![]() 上一动点,连结
上一动点,连结![]() ,
,![]() ,过
,过![]() 作
作![]() 于点
于点![]() .
.
(1)直接写出点![]() ,
,![]() 的坐标:
的坐标:![]() (______,______),
(______,______),![]() (______,______);
(______,______);
(2)当![]() 为
为![]() 中点时,求
中点时,求![]() 的长;
的长;
(3)当![]() 是以
是以![]() 为腰的等腰三角形时,求点
为腰的等腰三角形时,求点![]() 坐标;
坐标;
(4)当点![]() 在线段
在线段![]() (不与
(不与![]() ,
,![]() 重合)上运动时,作
重合)上运动时,作![]() 关于
关于![]() 的对称点
的对称点![]() ,若
,若![]() 落在
落在![]() 轴上,则
轴上,则![]() 的长为_______.
的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,已知点A(0,3),点B(![]() ,0),连接AB,若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
,0),连接AB,若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
(1)在点C1(﹣2,3+2![]() ),点C2(0,﹣2),点C3(3+
),点C2(0,﹣2),点C3(3+![]() ,﹣
,﹣![]() )中,线段AB的“等长点”是点________;
)中,线段AB的“等长点”是点________;
(2)若点D(m,n)是线段AB的“等长点”,且∠DAB=60°,求点D的坐标;
(3)若直线y=kx+3![]() k上至少存在一个线段AB的“等长点”,求k的取值范围.
k上至少存在一个线段AB的“等长点”,求k的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.

(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:①△AED≌△DFB;②S四边形BCDG=![]() ;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.
;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.
其中正确的结论个数为( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是宜宾市某周内最高气温的折线统计图,关于这7天的日气温的说法,错误的是( )
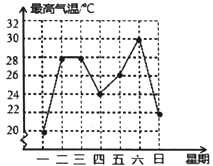
A.最高气温是30℃
B.最低气温是20℃
C.出现频率最高的是28℃
D.平均数是26℃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了丰富学生课余生活,开展了“第二课堂”活动,推出了以下四种选修课程:![]() 、绘画;
、绘画;![]() 、唱歌;
、唱歌;![]() 、演讲;
、演讲;![]() 、书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图,请结合统计图中的信息解决下列问题:
、书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图,请结合统计图中的信息解决下列问题:

(1)这次抽查的学生人数是多少人?
(2)将条形统计图补充完整;
(3)在扇形统计图中,求选课程![]() 的人数所对的圆心角的度数;
的人数所对的圆心角的度数;
(4)如果该校共有1200名学生,请你估计该校报课程![]() 的学生约有多少人?
的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①![]() ;②点F是GE的中点;③AF=
;②点F是GE的中点;③AF=![]() AB;④S△ABC=5S△BDF,其中正确的结论序号是( )
AB;④S△ABC=5S△BDF,其中正确的结论序号是( )
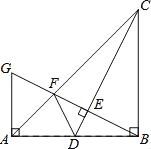
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
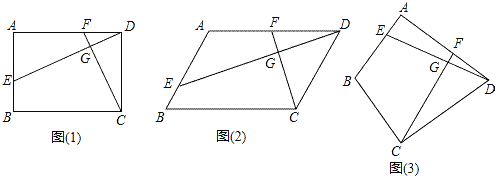
【题目】已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是矩形,且DE⊥CF.则DECD CFAD(填“<”或“=”或“>”);
(2)如图2,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得DECD=CFAD成立?并证明你的结论;
(3)如图3,若BA=BC=3,DA=DC=4,∠BAD=90°,DE⊥CF.则![]() 的值为 .
的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com