
【题目】如图,平面直角坐标系xOy中,已知点A(0,3),点B(![]() ,0),连接AB,若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
,0),连接AB,若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
(1)在点C1(﹣2,3+2![]() ),点C2(0,﹣2),点C3(3+
),点C2(0,﹣2),点C3(3+![]() ,﹣
,﹣![]() )中,线段AB的“等长点”是点________;
)中,线段AB的“等长点”是点________;
(2)若点D(m,n)是线段AB的“等长点”,且∠DAB=60°,求点D的坐标;
(3)若直线y=kx+3![]() k上至少存在一个线段AB的“等长点”,求k的取值范围.
k上至少存在一个线段AB的“等长点”,求k的取值范围.

【答案】(1)C1,C3;(2)D(﹣![]() ,0)或D(
,0)或D(![]() ,3);(3)﹣
,3);(3)﹣![]() ≤k≤
≤k≤![]()
【解析】
(1)直接利用线段AB的“等长点”的条件判断;
(2)分两种情况讨论,利用对称性和垂直的性质即可求出m,n;
(3)先判断出直线y=kx+3![]() 与圆A,B相切时,如图2所示,利用相似三角形的性质即可求出结论.
与圆A,B相切时,如图2所示,利用相似三角形的性质即可求出结论.
(1)∵A(0,3),B(![]() ,0),
,0),
∴AB=2![]() ,
,
∵点C1(﹣2,3+2![]() ),
),
∴AC1=![]() =2
=2![]() ,
,
∴AC1=AB,
∴C1是线段AB的“等长点”,
∵点C2(0,﹣2),
∴AC2=5,BC2=![]() =
=![]() ,
,
∴AC2≠AB,BC2≠AB,
∴C2不是线段AB的“等长点”,
∵点C3(3+![]() ,﹣
,﹣![]() ),
),
∴BC3=![]() =2
=2![]() ,
,
∴BC3=AB,
∴C3是线段AB的“等长点”;
故答案为:C1,C3;
(2)如图1,

在Rt△AOB中,OA=3,OB=![]() ,
,
∴AB=2![]() ,tan∠OAB=
,tan∠OAB=![]() =
=![]() ,
,
∴∠OAB=30°,
当点D在y轴左侧时,
∵∠DAB=60°,
∴∠DAO=∠DAB﹣∠BAO=30°,
∵点D(m,n)是线段AB的“等长点”,
∴AD=AB,
∴D(﹣![]() ,0),
,0),
∴m=![]() ,n=0,
,n=0,
当点D在y轴右侧时,
∵∠DAB=60°,
∴∠DAO=∠BAO+∠DAB=90°,
∴n=3,
∵点D(m,n)是线段AB的“等长点”,
∴AD=AB=2![]() ,
,
∴m=2![]() ;
;
∴D(![]() ,3)
,3)
(3)如图2,

∵直线y=kx+3![]() k=k(x+3
k=k(x+3![]() ),
),
∴直线y=kx+3![]() k恒过一点P(﹣3
k恒过一点P(﹣3![]() ,0),
,0),
∴在Rt△AOP中,OA=3,OP=3![]() ,
,
∴∠APO=30°,
∴∠PAO=60°,
∴∠BAP=90°,
当PF与⊙B相切时交y轴于F,
∴PA切⊙B于A,
∴点F就是直线y=kx+3![]() k与⊙B的切点,
k与⊙B的切点,
∴F(0,﹣3),
∴3![]() k=﹣3,
k=﹣3,
∴k=﹣![]() ,
,
当直线y=kx+3![]() k与⊙A相切时交y轴于G切点为E,
k与⊙A相切时交y轴于G切点为E,
∴∠AEG=∠OPG=90°,
∴△AEG∽△POG,
∴![]() ,
,
∴![]() =
=![]() ,解得:k=
,解得:k=![]() 或k=
或k=![]() (舍去)
(舍去)
∵直线y=kx+3![]() k上至少存在一个线段AB的“等长点”,
k上至少存在一个线段AB的“等长点”,
∴﹣![]() ≤k≤
≤k≤![]() ,
,


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣![]() x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,如果点
厘米,如果点![]() 以
以![]() 厘米
厘米![]() 的速度运动.
的速度运动.

(1)如果点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动.点
运动.点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点运动,它们同时出发,若点
点运动,它们同时出发,若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等:
的运动速度相等:
①经过“![]() 秒后,
秒后,![]() 和
和![]() 是否全等?请说明理由.
是否全等?请说明理由.
②当两点的运动时间为多少秒时,![]() 刚好是一个直角三角形?
刚好是一个直角三角形?
(2)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,点
的运动速度不相等,点![]() 从点
从点![]() 出发,点
出发,点![]() 以原来的运动速度从点
以原来的运动速度从点![]() 同时出发,都顺时针沿
同时出发,都顺时针沿![]() 三边运动,经过
三边运动,经过![]() 秒时点
秒时点![]() 与点
与点![]() 第一次相遇,则点
第一次相遇,则点![]() 的运动速度是__________厘米
的运动速度是__________厘米![]() 秒.(直接写出答案)
秒.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
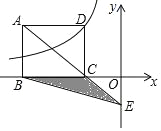
【题目】如图所示,矩形ABCD的顶点D在反比例函数![]() (x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,△BCE的面积是6,则k=_____.
(x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,△BCE的面积是6,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
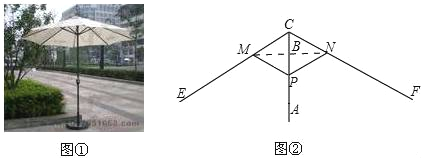
【题目】图1所示的遮阳伞,伞柄垂直于水平地面,其示意图如图2、当伞收紧时,点P与点A重合;当伞慢慢撑开时,动点P由A向B移动;当点P到达点B时,伞张得最开、已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米,CE=CF=18.0分米,BC=2.0分米、设AP=x分米.
(1)求x的取值范围;
(2)若∠CPN=60°,求x的值;
(3)设阳光直射下,伞下的阴影(假定为圆面)面积为y,求y关于x的关系式(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情景:如图1,在同一平面内,点![]() 和点
和点![]() 分别位于一块直角三角板
分别位于一块直角三角板![]() 的两条直角边
的两条直角边![]() ,
,![]() 上,点
上,点![]() 与点
与点![]() 在直线
在直线![]() 的同侧,若点
的同侧,若点![]() 在
在![]() 内部,试问
内部,试问![]() ,
,![]() 与
与![]() 的大小是否满足某种确定的数量关系?
的大小是否满足某种确定的数量关系?
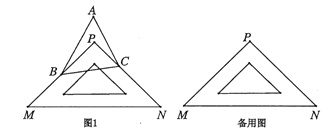
(1)特殊探究:若![]() ,则
,则![]() _________度,
_________度,![]() ________度,
________度,![]() _________度;
_________度;
(2)类比探索:请猜想![]() 与
与![]() 的关系,并说明理由;
的关系,并说明理由;
(3)类比延伸:改变点![]() 的位置,使点
的位置,使点![]() 在
在![]() 外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出
外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出![]() ,
,![]() 与
与![]() 满足的数量关系式.
满足的数量关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
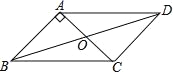
【题目】已知:如图,在ABCD中,对角线AC,BD交于点O,AB⊥AC,AB=1,BC=![]() .
.
(1)求平行四边形ABCD的面积S□ABCD;
(2)求对角线BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的角平分线.
的角平分线.
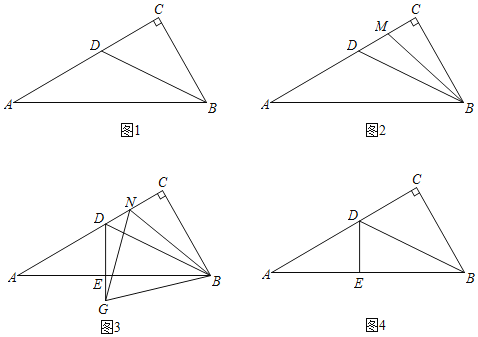
(1)如图 1,求证:![]() ;
;
(2)如图 2,作![]() 的角平分线交线段
的角平分线交线段![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;
(3)如图 3,过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 上一点(不与
上一点(不与 ![]() 重合),以
重合),以![]() 为一边,在
为一边,在![]() 的下方作
的下方作![]() ,
,![]() 交
交![]() 延长线于点
延长线于点![]() ,试探究线段
,试探究线段![]() ,
,![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
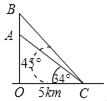
【题目】如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.
(1)求A,B两点间的距离(结果精确到0.1km).
(2)当运载火箭继续直线上升到D处,雷达站测得其仰角为56°,求此时雷达站C和运载火箭D两点间的距离(结果精确到0.1km).(参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com