
ЁОЬтФПЁПЮЪЬтЧщОАЃКШчЭМ1ЃЌдкЭЌвЛЦНУцФкЃЌЕу![]() КЭЕу
КЭЕу![]() ЗжБ№ЮЛгквЛПщжБНЧШ§НЧАх
ЗжБ№ЮЛгквЛПщжБНЧШ§НЧАх![]() ЕФСНЬѕжБНЧБп
ЕФСНЬѕжБНЧБп![]() ЃЌ
ЃЌ![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() гыЕу
гыЕу![]() дкжБЯп
дкжБЯп![]() ЕФЭЌВрЃЌШєЕу
ЕФЭЌВрЃЌШєЕу![]() дк
дк![]() ФкВПЃЌЪдЮЪ
ФкВПЃЌЪдЮЪ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЕФДѓаЁЪЧЗёТњзуФГжжШЗЖЈЕФЪ§СПЙиЯЕЃП
ЕФДѓаЁЪЧЗёТњзуФГжжШЗЖЈЕФЪ§СПЙиЯЕЃП
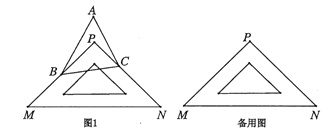
ЃЈ1ЃЉЬиЪтЬНОПЃКШє![]() ЃЌдђ
ЃЌдђ![]() _________ЖШЃЌ
_________ЖШЃЌ![]() ________ЖШЃЌ
________ЖШЃЌ![]() _________ЖШЃЛ
_________ЖШЃЛ
ЃЈ2ЃЉРрБШЬНЫїЃКЧыВТЯы![]() гы
гы![]() ЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉРрБШбгЩьЃКИФБфЕу![]() ЕФЮЛжУЃЌЪЙЕу
ЕФЮЛжУЃЌЪЙЕу![]() дк
дк![]() ЭтЃЌЦфЫќЬѕМўЖМВЛБфЃЌХаЖЯЃЈ2ЃЉжаЕФНсТлЪЧЗёШдШЛГЩСЂЃПШєГЩСЂЃЌЧыЫЕУїРэгЩЃЛШєВЛГЩСЂЃЌЧыжБНгаДГі
ЭтЃЌЦфЫќЬѕМўЖМВЛБфЃЌХаЖЯЃЈ2ЃЉжаЕФНсТлЪЧЗёШдШЛГЩСЂЃПШєГЩСЂЃЌЧыЫЕУїРэгЩЃЛШєВЛГЩСЂЃЌЧыжБНгаДГі![]() ЃЌ
ЃЌ![]() гы
гы![]() ТњзуЕФЪ§СПЙиЯЕЪНЃЎ
ТњзуЕФЪ§СПЙиЯЕЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉ125ЃЌ90ЃЌ35ЃЛЃЈ2ЃЉЁЯABP+ЁЯACP=90Ёу-ЁЯAЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉНсТлВЛГЩСЂЃЎЁЯABP-ЁЯACP=90Ёу-ЁЯAЃЌЁЯABP+ЁЯACP=ЁЯA-90ЁуЛђЁЯACP - ЁЯABP =90Ёу-ЁЯAЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнШ§НЧаЮФкНЧКЭМДПЩЕУГіЁЯABC+ЁЯACBЃЌЁЯPBC+ЁЯPCBЃЌШЛКѓМДПЩЕУГіЁЯABP+ЁЯACPЃЛ
ЃЈ2ЃЉИљОнШ§НЧаЮФкНЧКЭЖЈРэНјааЕШСПзЊЛЛЃЌМДПЩЕУГіЁЯABP+ЁЯACP=90Ёу-ЁЯAЃЛ
ЃЈ3ЃЉАДееЃЈ2ЃЉжаЭЌбљЕФЗНЗЈНјааЕШСПзЊЛЛЃЌЧѓНтМДПЩХаЖЈ.
ЃЈ1ЃЉЁЯABC+ЁЯACB=180Ёу-ЁЯA=180Ёу-55Ёу=125ЖШЃЌЁЯPBC+ЁЯPCB=180Ёу-ЁЯP=180Ёу-90Ёу=90ЖШЃЌ
ЁЯABP+ЁЯACP=ЁЯABC+ЁЯACB -ЃЈЁЯPBC+ЁЯPCBЃЉ=125Ёу-90Ёу=35ЖШЃЛ
ЃЈ2ЃЉВТЯыЃКЁЯABP+ЁЯACP=90Ёу-ЁЯAЃЛ
жЄУїЃКдкЁїABCжаЃЌЁЯABC+ЁЯACBЃН180Ёу-ЁЯAЃЌ
ЁпЁЯABC=ЁЯABP+ЁЯPBCЃЌЁЯACB=ЁЯACP+ЁЯPCBЃЌ
ЁрЃЈЁЯABP+ЁЯPBCЃЉ+ЃЈЁЯACP+ЁЯPCBЃЉ=180Ёу-ЁЯAЃЌ
ЁрЃЈЁЯABP+ЁЯACPЃЉ+ЃЈЁЯPBC+ЁЯPCBЃЉ=180Ёу-ЁЯAЃЌ
гжЁпдкRtЁїPBCжаЃЌЁЯP=90ЁуЃЌ
ЁрЁЯPBC+ЁЯPCB=90ЁуЃЌ
ЁрЃЈЁЯABP+ЁЯACPЃЉ+90Ёу=180Ёу-ЁЯAЃЌ
ЁрЁЯABP+ЁЯACP=90Ёу-ЁЯAЃЎ
ЃЈ3ЃЉХаЖЯЃКЃЈ2ЃЉжаЕФНсТлВЛГЩСЂЃЎ
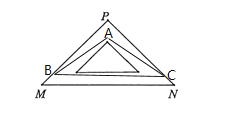
жЄУїЃКдкЁїABCжаЃЌЁЯABC+ЁЯACBЃН180Ёу-ЁЯAЃЌ
ЁпЁЯABC=ЁЯPBC-ЁЯABPЃЌЁЯACB=ЁЯPCB-ЁЯACPЃЌ
ЁрЃЈЁЯPBC+ЁЯPCBЃЉ-ЃЈЁЯABP+ЁЯACPЃЉ=180Ёу-ЁЯAЃЌ
гжЁпдкRtЁїPBCжаЃЌЁЯP=90ЁуЃЌ
ЁрЁЯPBC+ЁЯPCB=90ЁуЃЌ
ЁрЁЯABP-ЁЯACP=90Ёу-ЁЯAЃЌЁЯABP+ЁЯACP=ЁЯA-90Ёу
ЛђЁЯACP - ЁЯABP =90Ёу-ЁЯAЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
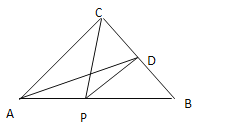
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌвдаББпABЩЯвЛЕуOЮЊдВаФЃЌOBЮЊАыОЖзїЁбOЃЌНЛACгкЕуEЃЌНЛABгкЕуDЃЌЧвЁЯBEC=ЁЯBDEЃЎ
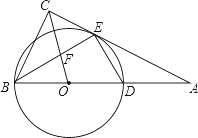
ЃЈ1ЃЉЧѓжЄЃКACЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉСЌНгOCНЛBEгкЕуFЃЌШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
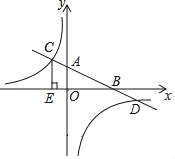
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпABЗжБ№гыxжсЁЂyжсНЛгкЕуBЃЌAЃЌгыЗДБШР§КЏЪ§ЕФЭМЯѓЗжБ№НЛгкЕуCЃЌDЃЌCEЁЭxжсгкЕуEЃЌtanЁЯABO=![]() ЃЌOB=4ЃЌOE=2ЃЎ
ЃЌOB=4ЃЌOE=2ЃЎ
ЃЈ1ЃЉЧѓИУЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓШ§НЧаЮCDEЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкФГаЁбЇЁАбнНВДѓШќЁБбЁАЮШќГѕШќжаЃЌМзЁЂввЁЂБћШ§ЮЛЦРЮЏЖдаЁбЁЪжЕФзлКЯБэЯжЃЌЗжБ№ИјГіЁАД§ЖЈЁБЃЈгУзжФИWБэЪОЃЉЛђЁАЭЈЙ§ЁБЃЈгУзжФИPБэЪОЃЉЕФНсТлЃЎ
ЃЈ1ЃЉЧыгУЪїзДЭМБэЪОГіШ§ЮЛЦРЮЏИјаЁбЁЪжчїчїЕФЫљгаПЩФмЕФНсТлЃЛ
ЃЈ2ЃЉЖдгкаЁбЁЪжчїчїЃЌжЛгаМзЁЂввСНЮЛЦРЮЏИјГіЯрЭЌНсТлЕФИХТЪЪЧЖрЩйЃП
ЃЈ3ЃЉБШШќЙцЖЈЃЌШ§ЮЛЦРЮЏжажСЩйгаСНЮЛИјГіЁАЭЈЙ§ЁБЕФНсТлЃЌдђаЁбЁЪжПЩШыЮЇНјШыИДШќЃЌЮЪчїчїНјШыИДШќЕФИХТЪЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊЕуAЃЈ0ЃЌ3ЃЉЃЌЕуBЃЈ![]() ЃЌ0ЃЉЃЌСЌНгABЃЌШєЖдгкЦНУцФквЛЕуCЃЌЕБЁїABCЪЧвдABЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌГЦЕуCЪЧЯпЖЮABЕФЁАЕШГЄЕуЁБЃЎ
ЃЌ0ЃЉЃЌСЌНгABЃЌШєЖдгкЦНУцФквЛЕуCЃЌЕБЁїABCЪЧвдABЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌГЦЕуCЪЧЯпЖЮABЕФЁАЕШГЄЕуЁБЃЎ
ЃЈ1ЃЉдкЕуC1ЃЈЉ2ЃЌ3+2![]() ЃЉЃЌЕуC2ЃЈ0ЃЌЉ2ЃЉЃЌЕуC3ЃЈ3+
ЃЉЃЌЕуC2ЃЈ0ЃЌЉ2ЃЉЃЌЕуC3ЃЈ3+![]() ЃЌЉ
ЃЌЉ![]() ЃЉжаЃЌЯпЖЮABЕФЁАЕШГЄЕуЁБЪЧЕу________ЃЛ
ЃЉжаЃЌЯпЖЮABЕФЁАЕШГЄЕуЁБЪЧЕу________ЃЛ
ЃЈ2ЃЉШєЕуDЃЈmЃЌnЃЉЪЧЯпЖЮABЕФЁАЕШГЄЕуЁБЃЌЧвЁЯDAB=60ЁуЃЌЧѓЕуDЕФзјБъЃЛ
ЃЈ3ЃЉШєжБЯпy=kx+3![]() kЩЯжСЩйДцдквЛИіЯпЖЮABЕФЁАЕШГЄЕуЁБЃЌЧѓkЕФШЁжЕЗЖЮЇЃЎ
kЩЯжСЩйДцдквЛИіЯпЖЮABЕФЁАЕШГЄЕуЁБЃЌЧѓkЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌEЪЧDCБпЩЯЕФЕуЃЌСЌНгBEЃЌНЋЁїBCEШЦЕуCЫГЪБеыЗНЯђа§зЊ90ЁуЕУЕНЁїDCFЃЌСЌНгEFЃЎШєЁЯEFD=15ЁуЃЌдђЁЯCDFЕФЖШЪ§ЮЊ__ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМAMЁЮBNЃЌCЪЧBNЩЯвЛЕуЃЌ BDЦНЗжЁЯABNЧвЙ§ACЕФжаЕуOЃЌНЛAMгкЕуDЃЌDEЁЭBDЃЌНЛBNгкЕуEЃЎ

ЃЈ1ЃЉЧѓжЄЃКЁїADOЁеЁїCBOЃЎ
ЃЈ2ЃЉЧѓжЄЃКЫФБпаЮABCDЪЧСтаЮЃЎ
ЃЈ3ЃЉШєDE = AB = 2ЃЌЧѓСтаЮABCDЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЪЧвЫБіЪаФГжмФкзюИпЦјЮТЕФелЯпЭГМЦЭМЃЌЙигкет7ЬьЕФШеЦјЮТЕФЫЕЗЈЃЌДэЮѓЕФЪЧЃЈ ЃЉ
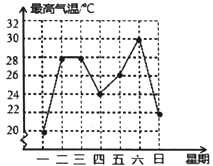
A.зюИпЦјЮТЪЧ30Ёц
B.зюЕЭЦјЮТЪЧ20Ёц
C.ГіЯжЦЕТЪзюИпЕФЪЧ28Ёц
D.ЦНОљЪ§ЪЧ26Ёц
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШбќжБНЧ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]()
![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЩЯЕФвЛИіЖЏЕуЃЌЕБ
ЩЯЕФвЛИіЖЏЕуЃЌЕБ![]() ЕудЫЖЏЪБЃЌ
ЕудЫЖЏЪБЃЌ![]() ЕФзюаЁжЕЮЊ____
ЕФзюаЁжЕЮЊ____
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com