
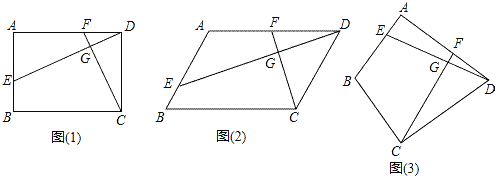
����Ŀ����֪�ı���ABCD�У�E��F�ֱ���AB��AD���ϵĵ㣬DE��CF���ڵ�G��
(1)��ͼ1�����ı���ABCD�Ǿ��Σ���DE��CF����DECD�� ��CFAD��������������=��������������
(2)��ͼ2�����ı���ABCD��ƽ���ı��Σ���̽��������B���EGC����ʲô��ϵʱ��ʹ��DECD=CFAD��������֤����Ľ��ۣ�
(3)��ͼ3����BA=BC=3��DA=DC=4����BAD=90�㣬DE��CF����![]() ��ֵΪ�� ����
��ֵΪ�� ����
���𰸡�(1)=��(2)����B+��EGC=180��ʱ��DECD=CFAD������֤����������(3)![]() ��
��
��������
���⣨1�����ݾ������ʵó���A=��FDC=90���������CFD=��AED��֤����AED�ס�DFC���ɣ�
��2������B+��EGC=180��ʱ��![]() ������֤��DFG�ס�DEA���ó�
������֤��DFG�ס�DEA���ó�![]() ��֤��CGD�ס�CDF���ó�
��֤��CGD�ס�CDF���ó�![]() �����ɵó��𰸣�
�����ɵó��𰸣�
��3����C��CN��AD��N��CM��AB��AB�ӳ�����M������BD����CN=x����BAD�ա�BCD���Ƴ���BCD=��A=90����֤��BCM�ס�DCN�����CM=x����Rt��CMB�У��ɹ��ɶ����ó�![]() ������ó�����
���������![]() �����CN=
�����CN=![]() ��֤����AED�ס�NFC�����ɵó��𰸣�
��֤����AED�ס�NFC�����ɵó��𰸣�
�����������1��֤�������ı���ABCD�Ǿ��Σ�
���A=��FDC=90����
��CF��DE��
���DGF=90����
���ADE+��CFD=90������ADE+��AED=90����
���CFD=��AED��
�ߡ�A=��CDF��
���AED�ס�DFC��
��![]() ����
����![]() =
=![]() .
.
��2������B+��EGC=180��ʱ��![]() =
=![]() ������
������
֤�������ı���ABCD��ƽ���ı��Σ�
���B=��ADC��AD��BC��
���B+��A=180����
�ߡ�B+��EGC=180����
���A=��EGC=��FGD��
�ߡ�FDG=��EDA��
���DFG�ס�DEA��
��![]() ��
��
�ߡ�B=��ADC����B+��EGC=180������EGC+��DGC=180����
���CGD=��CDF��
�ߡ�GCD=��DCF��
���CGD�ס�CDF��
��![]() ��
��
��![]() ��
��
��![]() ��
��
������B+��EGC=180��ʱ��![]() ������
������
��3���⣺![]() ��
��
�����ǣ���C��CN��AD��N��CM��AB��AB�ӳ�����M������BD����CN=x��
��AB��AD��
���A=��M=��CNA=90����
���ı���AMCN�Ǿ��Σ�
��AM=CN��AN=CM��
������BAD����BCD��
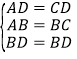
���BAD�ա�BCD��SSS����
���BCD=��A=90����
���ABC+��ADC=180����
�ߡ�ABC+��CBM=180����
���CBM=��ADC��
�ߡ�CND=��M=90����
���BCM�ס�DCN��
��![]() ��
��
��![]()
��![]()
��Rt��CMB�У�![]() ��BM=AM��AB=x��6���ɹ��ɶ����ã�
��BM=AM��AB=x��6���ɹ��ɶ����ã�![]() ��
��
��![]() ��
��
��� x=0����ȥ����x=![]()
��CN=![]() ��
��
�ߡ�A=��FGD=90����
���AED+��AFG=180����
�ߡ�AFG+��NFC=180����
���AED=��CFN��
�ߡ�A=��CNF=90����
���AED�ס�NFC��
��![]()
����: �����������ۺ���.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�
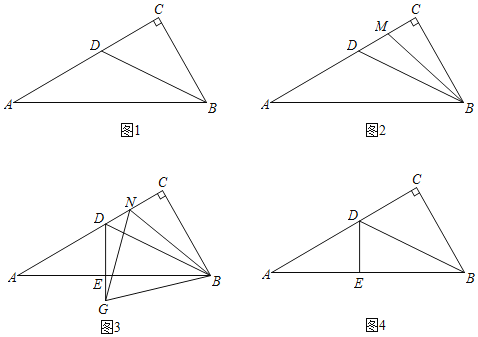
��1����ͼ 1����֤��![]() ��
��
��2����ͼ 2����![]() �Ľ�ƽ���߽��߶�
�Ľ�ƽ���߽��߶�![]() �ڵ�
�ڵ�![]() ����
����![]() ����
����![]() �������
�������
��3����ͼ 3������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ���߶�
���߶�![]() ��һ�㣨����
��һ�㣨���� ![]() �غϣ�����
�غϣ�����![]() Ϊһ�ߣ���
Ϊһ�ߣ���![]() ���·���
���·���![]() ��
��![]() ��
��![]() �ӳ����ڵ�
�ӳ����ڵ�![]() ����̽���߶�
����̽���߶�![]() ,
,![]() ��
��![]() ֮���������ϵ����˵�����ɣ�
֮���������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
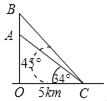
����Ŀ����ͼ��һö���ػ���Ӿ��״�վC��5km�ĵ���O�����䣬����������A��Bʱ�����״�վC��õ�A��B�����Ƿֱ�Ϊ34�㣬45�������е�O��A��B��ͬһ��ֱ���ϣ�
��1����A��B�����ľ��루�����ȷ��0.1km����
��2�������ػ������ֱ��������D�����״�վ���������Ϊ56�������ʱ�״�վC�����ػ��D�����ľ��루�����ȷ��0.1km�������ο����ݣ�sin34��=0.56��cos34��=0.83��tan34��=0.67����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ����С����������ѹǿʵ��ʱ�����ѹǿp(Pa)�����V(cm3)֮�������ж�Ӧ���ݣ�
p(Pa) | �� | 1 | 2 | 3 | 4 | 5 | �� |
V(cm3) | �� | 6 | 3 | 2 | 1.5 | 1.2 | �� |
���ݱ����ṩ����Ϣ���ش��������⣺
(1)����p��V֮��Ĺ�ϵ�������������ϵʽ��
(2)������������12cm3ʱ��ѹǿ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() �У�
�У�![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��
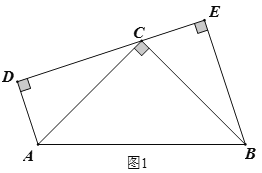
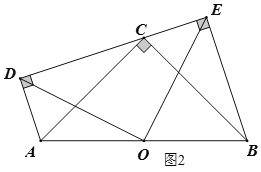
��1����ͼ1����֤��![]() ��
��
��2����ͼ2����![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() .���ж�
.���ж�![]() ����״����˵��������
����״����˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
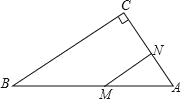
����Ŀ����ͼ���� Rt��ABC �У���C��90�㣬��A��60�㣬AB��10cm������M �ӵ� B ������ 2cm/s ���ٶ���� A �˶����� N �ӵ� A ������ 1cm/s ���ٶ���� C �˶����� M��N �ֱ�ӵ� B��A ͬʱ�������˶���ʱ��Ϊ ts��
��1���ú� t ��ʽ�ӱ�ʾ�߶� AM��AN �ij���
��2���� t Ϊ��ֵʱ����AMN ���� MN Ϊ�ױߵĵ��������Σ�
��3���� t Ϊ��ֵʱ��MN��BC���������ʱ CN �ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���A��y���������ϣ���B������Ϊ��0����3��������������y=��![]() ��ͼ����C��
��ͼ����C��
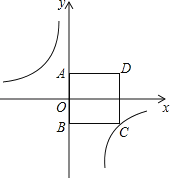
��1�����C�����ꣻ
��2������P�Ƿ���������ͼ���ϵ�һ����S��PAD=S������ABCD�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AB�ǡ�O��ֱ������CD��AB��H����CD�ӳ�����һ��E����O�����߽�AB���ӳ�����F���е�ΪG������AG��CD��K��
��1����ͼ1����֤��KE=GE��
��2����ͼ2������CABG������FGB=![]() ��ACH����֤��CA��FE��
��ACH����֤��CA��FE��
��3����ͼ3���ڣ�2���������£�����CG��AB�ڵ�N����sinE=![]() ��AK=
��AK=![]() ����CN�ij���
����CN�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��DE��AB��E��DF��AC��F����BD��CD��BE��CF�������н��ۣ���DE��DF����ADƽ�֡�BAC����AE��AD����AC��AB��2BE����ȷ����_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com