
【题目】如图,在三角形ABC中, ∠B=60°, ∠C=![]() ,点D是AB上一点,点E是AC上一点, ∠ADE=60°, 点F为线段BC上一点,连接EF,过D作DG//AC交EF于点G,
,点D是AB上一点,点E是AC上一点, ∠ADE=60°, 点F为线段BC上一点,连接EF,过D作DG//AC交EF于点G,
(1)若![]() =40°,求∠EDG的度数;
=40°,求∠EDG的度数;
(2)若∠FEC=2∠DEF,∠DGF=![]() ∠BFG,求
∠BFG,求![]() .
.

【答案】(1)40°;(2)72°
【解析】
(1)根据同位角相等即可判断出DE∥BC,根据平行线的性质即可求解;
(2)设∠DEF=x°,∠FEC=2x°,根据平行线的性质得∠DGE=∠FEC=2x° ,DEF=∠EFC=x°,分别表示出∠DGF、∠BFG,可得关于x的方程,解方程求得x的值,由三角形的内角和即可求解.
(1)∵∠B=∠ADE=60°
∴DE∥BC
∴∠C=∠AED=40°
又DG∥AC
∴∠GDE=∠AED=40°;
(2)∵∠FEC=2∠DEF
∴设∠DEF=x°,∠FEC=2x°
∵DG∥BC
∴∠DGE=∠FEC=2x°
∴∠DGF=(180-2x)°
又DE∥BC
∴∠DEF=∠EFC=x°
∴∠BFG=(180-x)°
又∠DGF=![]() ∠BFG
∠BFG
∴180-2x=![]() (180-x)
(180-x)
∴x=36,
∴∠EFC=x°=36°,∠FEC=2x°=72°,
∴∠C=α=180°-∠EFC -∠FEC =72°.
故答案为:(1)40°;(2)72°.


科目:初中数学 来源: 题型:
【题目】已知点P(x0 , y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d= ![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y= ![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.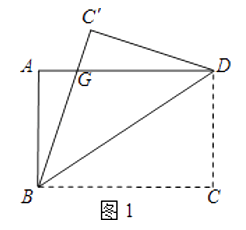
(1)求证:AG=C′G;
(2)如图2,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,求EM的长.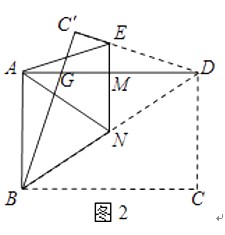
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中:①有限小数是有理数;②无限小数都是无理数;③任意两个无理数的和还是无理数;④开方开不尽的数是无理数;⑤一个数的算术平方根一定是正数;⑥一个数的立方根一定比这个数小;⑦任意两个有理数之间都有有理数,任意两个无理数之间都有无理数.⑧有理数和数轴上的点一一对应;⑨不带根号的数一定是有理数;⑩负数没有立方根.其中正确的有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=9,AC=12.分别以点A和点B为圆心、大于AB一半的长为半径作圆弧,两弧相交于点E和点F,作直线EF交AB于点D,连结CD.则CD的长为 . 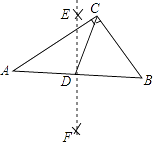
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两条长度均为2的线段![]() 和线段
和线段![]() 互相重合,将
互相重合,将![]() 沿直线
沿直线![]() 向左平移
向左平移![]() 个单位长度,将
个单位长度,将![]() 沿直线
沿直线![]() 向右也平移
向右也平移![]() 个单位长度,当
个单位长度,当![]() 、
、![]() 是线段
是线段![]() 的三等分点时,则
的三等分点时,则![]() 的值为________.
的值为________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y= ![]() (x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
(x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
①双曲线的解析式为y= ![]() (x>0);②E点的坐标是(5,8);③sin∠COA=
(x>0);②E点的坐标是(5,8);③sin∠COA= ![]() ;④AC+OB=12
;④AC+OB=12 ![]() .其中正确的结论有( )
.其中正确的结论有( )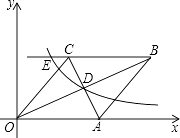
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com