
【题目】已知点P(x0 , y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d= ![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y= ![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
【答案】
(1)解:因为直线y=x﹣1,其中k=1,b=﹣1,
所以点P(1,﹣1)到直线y=x﹣1的距离为:d= ![]() =
= ![]() =
= ![]() =
= ![]()
(2)解:⊙Q与直线y= ![]() x+9的位置关系为相切.
x+9的位置关系为相切.
理由如下:
圆心Q(0,5)到直线y= ![]() x+9的距离为:d=
x+9的距离为:d= ![]() =
= ![]() =2,
=2,
而⊙O的半径r为2,即d=r,
所以⊙Q与直线y= ![]() x+9相切
x+9相切
(3)解:当x=0时,y=﹣2x+4=4,即点(0,4)在直线y=﹣2x+4,
因为点(0,4)到直线y=﹣2x﹣6的距离为:d= ![]() =
= ![]() =2
=2 ![]() ,
,
因为直线y=﹣2x+4与y=﹣2x﹣6平行,
所以这两条直线之间的距离为2 ![]()
【解析】(1)根据点P到直线y=kx+b的距离公式直接计算即可;
(2)先利用点到直线的距离公式计算出圆心Q到直线y=![]() x+9,然后根据切线的判定方法可判断 Q与直线y=
x+9,然后根据切线的判定方法可判断 Q与直线y=![]() x+9相切;
x+9相切;
(3)利用两平行线间的距离定义,在直线y=-2x+4上任意取一点,然后计算这个点到直线y=-2x-6的距离即可.
【考点精析】通过灵活运用切线的判定定理,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】为了解某地区电视观众对新闻、动画、娱乐三类节目的喜爱情况,根据老年人、中年人、青少年各年龄段实际人口的比例,按3:5:2随机抽取一定数量的观众进行调查,得到如下统计图.
(1)上面所用的调查方法是(填“普查”或“抽样调查”).
(2)写出折线统计图中A所代表的值是 .
(3)求该地区被调查的观众中,喜爱娱乐类节目的中年人的人数.
(4)根据以上统计图提供的信息,请你简要分析该地区电视观众对新闻、动画、娱乐三类节目的喜爱情况(字数不超过30字).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
查看答案和解析>>
科目:初中数学 来源: 题型:
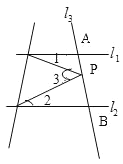
【题目】如图,已知直线11∥12,且13和11、12分别交于A、B两点,点P在直线AB上.
(1)试猜想写出∠1,∠2,∠3之间的关系式,并加以证明.
(2)如果点P在A、B两点外侧(点P和A、B不重合)运动时,试画出图形,写出∠1,∠2,∠3之间的关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,反比例函数y=![]() (x<0)的图象经过矩形OABC的对角线AC的中点M,分别与AB,BC交于点D、E,若BD=3,OA=4,则k的值为_____.
(x<0)的图象经过矩形OABC的对角线AC的中点M,分别与AB,BC交于点D、E,若BD=3,OA=4,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校初三学生英语口语检测成绩等级的分布情况,随机抽取了该校若干名学生的英语口语检测成绩,按A,B,C,D四个等级进行统计分析,并绘制可如下尚不完整的统计图;请根据以上统计图提供的信息,解答下列问题:
(1)本次抽取的学生有名;
(2)补全条形统计图;
(3)在抽取的学生中C级人数所占的百分比是;
(4)根据抽样调查结果,请你估计某校860名初三学生英语口语检测成绩等级为A级的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形ABC中, ∠B=60°, ∠C=![]() ,点D是AB上一点,点E是AC上一点, ∠ADE=60°, 点F为线段BC上一点,连接EF,过D作DG//AC交EF于点G,
,点D是AB上一点,点E是AC上一点, ∠ADE=60°, 点F为线段BC上一点,连接EF,过D作DG//AC交EF于点G,
(1)若![]() =40°,求∠EDG的度数;
=40°,求∠EDG的度数;
(2)若∠FEC=2∠DEF,∠DGF=![]() ∠BFG,求
∠BFG,求![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com