
����Ŀ��Ϊ�˽�ij�������ӹ��ڶ����š����������������Ŀ��ϲ����������������ˡ������ˡ�������������ʵ���˿ڵı�������3��5��2�����ȡһ�������Ĺ��ڽ��е��飬�õ�����ͳ��ͼ��
��1���������õĵ��鷽��������ղ顱�������顱����
��2��д������ͳ��ͼ��A��������ֵ�� ��
��3����õ���������Ĺ����У�ϲ���������Ŀ�������˵�������
��4����������ͳ��ͼ�ṩ����Ϣ�������Ҫ�����õ������ӹ��ڶ����š����������������Ŀ��ϲ�����������������30�֣���
���𰸡�
��1����������
��2��68
��3���⣺����������Ϊ94+46+40=180��180�� ![]() =600�ˣ�
=600�ˣ�
����ȡ����Ϊ600�ˣ�
������������Ϊ600�� ![]() =300��
=300��
��ϲ���������Ŀ�������˵�����300�� ![]() =90��
=90��
��4���⣺�õ������ӹ��ڶ����š����������������Ŀ��ϲ������ǣ�������ϲ�����Ž�Ŀ�Ľ϶࣬������ϲ��������Ŀ�Ľ϶�
���������⣺��1���������飻���Դ��ǣ��������飻��2��A=68�����Դ��ǣ�68��
�����㾫����������Ҫ������ȫ�������������������ͳ��ͼ�����֪ʶ�㣬��Ҫ����ȫ������ռ���������ȫ�桢ȷ����һ�㻨�Ѷࡢ��ʱ��������ijЩ���鲻����ȫ����飻����������л����١�ʡʱ���ص㣬����ȡ�������Ƿ���д����ԣ�ֱ�ӹ�ϵ����������Ƶ�ȷ�̶ȣ�������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯���������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij�ֵ綯���������ܣ������ֵ綯���������˳�죬��һ�γ�����ʻ���������Ϊ A��B��C��D �ĸ��ȼ���������Ӧ�ȼ����������Ϊ 200 ǧ�ף�210 ǧ�ף�220ǧ�ף�230 ǧ�ף�������²�������ͳ��ͼ��
����������Ϣ������������⣺
��1������α����ĵ綯�������м���������ȫ����ͳ��ͼ��
��2���������ֵ綯����һ�γ�����ʻ��ƽ�������Ϊ����ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У���C=90�㣬AC=BC=![]() ������ABC�Ƶ�A˳ʱ�뷽����ת60�㵽��AB��C����λ�ã�����C��B����C��B�ij�Ϊ��������
������ABC�Ƶ�A˳ʱ�뷽����ת60�㵽��AB��C����λ�ã�����C��B����C��B�ij�Ϊ��������

A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ�ڼ���122��892ʱ������������̽������λ����ƽ�����з��ݵļ��㷽����������̽�����ü�������֤��������ѧ֪ʶ���ͣ��ó�����λ����ƽ������������ʽ���㷨�����м��㣬�磺

���е�һ�е���01������04���ֱ���ʮλ����λ����ƽ������ռ����λ�ã�����������λ�ľ�����ʮλ��λ���Ϸ�����0�����ٰ����Dz��� ���У��ڶ��е���04��Ϊʮλ�����λ������2����ռ����λ�ã�����������λ�ľ�����ʮλ��λ���Ϸ�����0�����ٰ����ǰ��������ʽ��Ӿ͵õ���12 2 =144.���е�һ�е���64������81���ֱ���ʮλ����λ����ƽ������ռ����λ�ã��ٰ����Dz������У��ڶ��е���144��Ϊʮλ�����λ������2�����ٰ����ǰ��������ʽ��Ӿ͵õ���892 =7921.
��������������������752 ��682(д������ʽ����������)
����������ѧ֪ʶ������������λ��ƽ������ʽ���㷨��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������� ����
��1�����䷽����һԪ���η��̣�2x2��4x��5=0��
��2������ ![]() �£�x+2��
�£�x+2�� ![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��BC���ϵĸߣ���B��30������ACB��100����AEƽ�֡�BAC�����EAD�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı�������E�DZ�CD��һ������BC��EC��CF��BE��AB�ڵ�F��P��EB�ӳ�����һ�������н��ۣ���BEƽ����CBF����CFƽ����DCB����BC��FB����PF��PC��������ȷ���۵ĸ���Ϊ( )
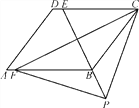
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���ABCD�ı�AD��x���ϣ���C��y��ĸ������ϣ�ֱ��BC��AD����BC��3��OD��2��������A��B�����ֱ��l��y����2x��10����ƽ�ƣ�ƽ�ƺ��ֱ����x�ύ�ڵ�E����ֱ��BC���ڵ�F����AE�ij�Ϊt��t��0����
��1���ı���ABCD�����Ϊ�� ��������ʾ��Сѧ��ѧ������������㷽����
��2�����ı���ABCD��ֱ��lɨ�����������Ӱ���֣�ΪS����д��S����t�ĺ�������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��x0 �� y0����ֱ��y=kx+b�����P��ֱ��y=kx+b�ľ���֤�����ù�ʽd= ![]() ���㣮
���㣮
���磺���P����1��2����ֱ��y=3x+7�ľ��룮
�⣺��Ϊֱ��y=3x+7������k=3��b=7��
���Ե�P����1��2����ֱ��y=3x+7�ľ���Ϊ��d= ![]() =
= ![]() =
= ![]() =
= ![]() ��
��
�������ϲ��ϣ�����������⣺
��1�����P��1����1����ֱ��y=x��1�ľ��룻
��2����֪��Q��Բ��Q����Ϊ��0��5�����뾶rΪ2���жϡ�Q��ֱ��y= ![]() x+9��λ�ù�ϵ��˵�����ɣ�
x+9��λ�ù�ϵ��˵�����ɣ�
��3����ֱ֪��y=��2x+4��y=��2x��6ƽ�У���������ֱ��֮��ľ��룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com