
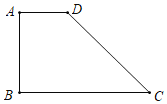
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,AB=4,BC=6,点O是边BC上一点,以O为圆心,OC为半径的⊙O,与边AD只有一个公共点,则OC的取值范围是( )
A. 4<OC≤![]() B. 4≤OC≤
B. 4≤OC≤![]() C. 4<OC
C. 4<OC![]() D. 4≤OC
D. 4≤OC![]()
【答案】B
【解析】
作DE⊥BC于E,当⊙O与边AD相切时,圆心O与E重合,即OC=4;当OA=OC时,⊙O与AD交于点A,设OA=OC=x,则OB=6﹣x,在Rt△ABO中,由勾股定理得出方程,解方程得出OC=![]() ;即可得出结论.
;即可得出结论.
作DE⊥BC于E,如图所示:
则DE=AB=4,BE=AD=2,
∴CE=4=DE,
当⊙O与边AD相切时,切点为D,圆心O与E重合,即OC=4;
当OA=OC时,⊙O与AD交于点A,
设OA=OC=x,则OB=6﹣x,
在Rt△ABO中,由勾股定理得:42+(6﹣x)2=x2,
解得:x=![]() ;
;
∴以O为圆心,OC为半径的⊙O,与边AD只有一个公共点,则OC的取值范围是4≤x≤![]() ;
;
故选:B.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
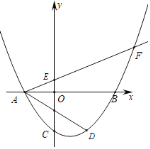
【题目】如图,在平面直角坐标系xOy中,已知抛物线![]() 与x轴交于点A、
与x轴交于点A、![]() 在B左侧
在B左侧![]() ,与y轴交于点C,经过点A的射线AF与y轴正半轴相交于点E,与抛物线的另一个交点为F,
,与y轴交于点C,经过点A的射线AF与y轴正半轴相交于点E,与抛物线的另一个交点为F,![]() ,点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且
,点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且![]() ,则点P的坐标是______.
,则点P的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意抛掷一枚质地均匀的正方体骰子2次,骰子的6个面上分别刻有1到6的点数,记第一次掷得面朝上的点数为横坐标,第二次掷得面朝上的点数为纵坐标,这样组成的点的坐标恰好在正比例函数y=x上的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
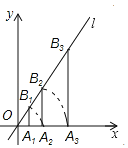
【题目】如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y=![]() x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2,则点A2的坐标为_____;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则
x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2,则点A2的坐标为_____;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则![]() 的长是_____.
的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
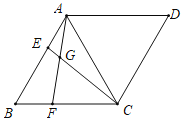
【题目】已知:如图,在菱形ABCD中,AB=AC,点E、F分别在边AB、BC上,且AE=BF,CE与AF相交于点G.
(1)求证:∠FGC=∠B;
(2)延长CE与DA的延长线交于点H,求证:BECH=AFAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
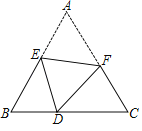
【题目】如图,将等边三角形ABC折叠,使得点A落在BC边上的点D处,折痕为EF,点E,F分别在AB和AC边上.若AB=6,BD=2,则AE:AF的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
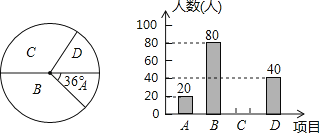
【题目】某学校为了提高学生学科能力,决定开设以下校本课程:A.文学院;B.小小数学家;C.小小外交家;D、未来科学家.为了了解学生最喜欢哪一项校本课程,学校随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次统计共抽查了 名学生;在扇形统计图中,表示C类别的扇形圆心角度数为 .
(2)补全条形统计图;
(3)一班想从表达能力很强的甲、乙、丙、丁四名同学中,任选2名参加小小外交家小组,请用列表或画树状图的方法求恰好同时选中甲、乙两名同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com