
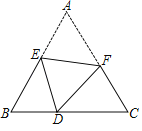
【题目】如图,将等边三角形ABC折叠,使得点A落在BC边上的点D处,折痕为EF,点E,F分别在AB和AC边上.若AB=6,BD=2,则AE:AF的值为_____.
【答案】![]()
【解析】
由已知求得CD=3a,根据等边三角形的性质和折叠的性质可得:BE+DE+BD=8,DF+CF+CD=10,再证明△BED∽△CDF,由相似三角形周长的比等于相似比,即可得出结果.
∵△ABC是等边三角形,
∴BC=AB=AC=6,∠ABC=∠ACB=∠BAC=60°,
∵BD=2,
∴CD=4,
由折叠的性质可知:AE=DE,AF=DF,∠EDF=∠A=60°,
∴BE+DE+BD=AB+BD=8,DF+CF+CD=AC+CD=10,
∵∠EDF=∠BAC=∠ABC=60°,
∴∠FDC+∠EDB=∠BED+∠EBD=120°,
∴∠FDC=∠BED,
∵∠B=∠C=60°,
∴△BED∽△CDF,
∴(BE+DE+BD):(DF+CF+CD)=DE:DF=AE:AF,
∴![]()
故答案为:![]() .
.


科目:初中数学 来源: 题型:
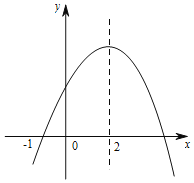
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)2a+b=0;(2)9a+c>3b;(3)5a+7b+2c>0;(4)若点A(-3,y1)、点B(![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y2<y3;(5)若方程a(x+1)(x-5)=c的两根为x1和x2,且x1<x2,则x1<-1<5<x2,其中正确的结论有( )
,y3)在该函数图象上,则y1<y2<y3;(5)若方程a(x+1)(x-5)=c的两根为x1和x2,且x1<x2,则x1<-1<5<x2,其中正确的结论有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
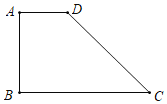
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,AB=4,BC=6,点O是边BC上一点,以O为圆心,OC为半径的⊙O,与边AD只有一个公共点,则OC的取值范围是( )
A. 4<OC≤![]() B. 4≤OC≤
B. 4≤OC≤![]() C. 4<OC
C. 4<OC![]() D. 4≤OC
D. 4≤OC![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
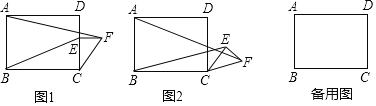
【题目】如图1,在矩形ABCD中,AB=6,BC=8,点E是边CD上的点,且CE=4,过点E作CD的垂线,并在垂线上截取EF=3,连接CF.将△CEF绕点C按顺时针方向旋转,记旋转角为a.
(1)问题发现
当a=0°时,AF= ,BE= ,![]() = ;
= ;
(2)拓展探究
试判断:当0°≤a°<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△CEF旋转至A,E,F三点共线时,直接写出线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM,垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)求证:AM是⊙O的切线;
(2)若⊙O的半径为4,求图中阴影部分的面积(结果保留π和根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”译文:“今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?”设每只雀重x斤,每只燕重y斤,可列方程组为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点P(a,b)关于原点的对称点为P′,以PP′为边作等边△PP′C,则称点C为P的“等边对称点”;
(1)若P(1,3),求点P的“等边对称点”的坐标.
(2)平面内有一点P(1,2),若它其中的一个“等边对称点”C在第四象限时,请求此C点的坐标;
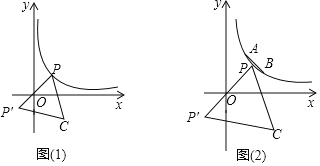
(3)若P点是双曲线y=![]() (x>0)上一动点,当点P的“等边对称点”点C在第四象限时,
(x>0)上一动点,当点P的“等边对称点”点C在第四象限时,
①如图(1),请问点C是否也会在某一函数图象上运动?如果是,请求出此函数的解析式;如果不是,请说明理由.
②如图(2),已知点A (1,2),B (2,1),点G是线段AB上的动点,点F在y轴上,若以A、G、F、C这四个点为顶点的四边形是平行四边形时,求点C的纵坐标yc的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3![]() ,求弦AD的长.
,求弦AD的长.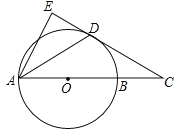
查看答案和解析>>
科目:初中数学 来源: 题型:
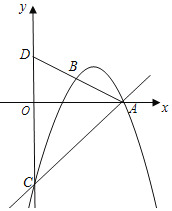
【题目】如图,抛物线y=ax2+4x+c过点A(6,0)、B(3,![]() ),与y轴交于点C.联结AB并延长,交y轴于点D.
),与y轴交于点C.联结AB并延长,交y轴于点D.
(1)求该抛物线的表达式;
(2)求△ADC的面积;
(3)点P在线段AC上,如果△OAP和△DCA相似,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com