
【题目】已知两个分别含有30°,45°角的一副直角三角板.
(1)如图1叠放在一起
若OC恰好平分∠AOB,则∠AOD= 度;
若∠AOC=40°,则∠BOD= 度;
(2)如图2叠放在一起,∠AOD=4∠BOC,试计算∠AOC的度数.

【答案】(1)135,40;(2)∠AOC的度数为110°.
【解析】
(1)①根据角平分线的定义求出∠AOC,再根据∠AOD=∠AOC+∠COD代入数据进行计算即可得解;
②由已知可求得∠BOC,再根据∠BOD=∠COD-∠BOC代入数据进行计算即可得解;
(2)由已知可求得∠BOD,再根据∠AOC=∠AOB+∠COD-∠BOD代入数据进行计算即可得解.
(1)①∵OC平分∠AOB,∠AOB=90°,
∴∠AOC=![]() ∠AOB=45°,
∠AOB=45°,
∴∠AOD=∠AOC+∠COD=45°+90°=135°;
②由已知∠BOC=90°-∠40°=50°,
∴∠BOD=∠COD-∠BOC=90°-50°=40°,
故答案为:135,40
(2)∵∠AOD=4∠BOC,
∴∠AOB-∠BOD=4(∠COD-∠BOD),
即90°-∠BOD=4(-30°∠BOD),解得:∠BOD=10°,
∴∠AOC=∠AOB+∠COD-∠BOD=90°+30°-10°=110°
即∠AOC的度数为110°.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】一架飞机在两城之间飞行,风速为24千米/小时,顺风飞行需2小时50分,逆风飞行需要3小时.
(1)求无风时飞机的飞行速度;
(2)求两城之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣2,0),点B的坐标为(0,n),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC.则点C的坐标是_____(用字母n表示).
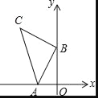
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某电脑公司有A型、B型、C型三种型号的电脑,其价格分别为A型每台6 000元,B型每台4 000元,C型每台2 500元,我市东坡中学计划将100 500元钱全部用于该电脑公司购进其中两种不同型号的电脑共36台,请你设计出几种不同的购买方案供该校选择,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC. 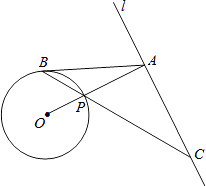
(1)求证:AB是⊙O的切线;
(2)PC=2 ![]() ,OA=4. ①求⊙O的半径;
,OA=4. ①求⊙O的半径;
②求线段PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)…按这样的运动规律,经过第2015次运动后,动点P的坐标是____.
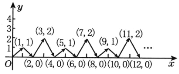
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC= ![]() ,∠DCE=
,∠DCE= ![]() .
.
① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时![]() 与
与![]() 之间的数量关系(不需证明).
之间的数量关系(不需证明).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com