
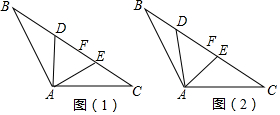
分析 (1)如图1,连接AF,根据等腰三角形的性质得到AF⊥BC,BF=CF,∠BAF=∠CAF=60°,∠B=∠C=30°,∠DAF=30°,根据等腰三角形的判定得到BD=AD,根据直角三角形的性质即可得到结论;
(2)如图2,连接AF,过D作DG⊥AB于G,过E作EH⊥AC于H,根据直角三角形的性质得到DG=$\frac{1}{2}$BD,EH=$\frac{1}{2}$CE,根据相似三角形的判定和性质即可得到结论.
解答 解:(1)如图1,连接AF,
∵AB=AC,点F是BC的中点,
∴AF⊥BC,BF=CF,
∵∠BAC=120°,
∴∠BAF=∠CAF=60°,∠B=∠C=30°,
∵DF=EF,
∴AD=AE,∵∠DAE=60°,
∴∠DAF=30°,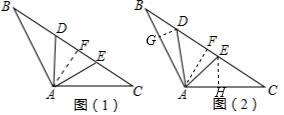
∠B=∠DAF,
∴BD=AD,
∵$\frac{AD}{DF}$=$\frac{1}{2}$,
∴$\frac{BD}{DF}$=$\frac{1}{2}$,同理$\frac{CE}{EF}$=$\frac{1}{2}$;
故答案为:$\frac{1}{2}$,$\frac{1}{2}$;
(2)如图2,连接AF,过D作DG⊥AB于G,过E作EH⊥AC于H,
∵∠B=∠C=30°,
∴DG=$\frac{1}{2}$BD,EH=$\frac{1}{2}$CE,
∵∠BAF=∠EAE=60°,
∴∠GAD=∠EAF,
∵∠EGA=∠AFE=90°,
∴△ADG∽△AEF,
∴$\frac{DG}{EF}=\frac{AD}{AE}$,
即$\frac{\frac{1}{2}BD}{EF}=\frac{AD}{AE}$,
同理$\frac{DF}{\frac{1}{2}CE}$=$\frac{AD}{AE}$,
∴$\frac{\frac{1}{2}BD}{EF}=\frac{DF}{\frac{1}{2}CE}$,
∴BD•CE=4DF•FE.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,直角三角形的性质,熟练掌握相似三角形的性质和判定是解题的关键.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
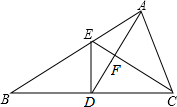 在△ABC中,D是BC的中点,DE⊥BC与AB相交于点E,且AD=AC,EC与AD相交于点F.
在△ABC中,D是BC的中点,DE⊥BC与AB相交于点E,且AD=AC,EC与AD相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
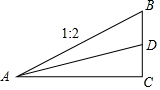 一段斜坡路面的截面图如图所示,BC⊥AC,其中坡面AB的坡比i1=1:2,现计划削坡放缓,新坡面的坡角为原坡面坡脚的一半,求新坡面AD的坡比i2(结果保留根号)
一段斜坡路面的截面图如图所示,BC⊥AC,其中坡面AB的坡比i1=1:2,现计划削坡放缓,新坡面的坡角为原坡面坡脚的一半,求新坡面AD的坡比i2(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
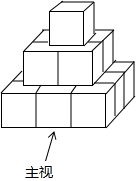 把棱长为1cm的若干个小正方体摆成如图所示的立体图形,然后在露出的表面上涂上颜色(不含底面).
把棱长为1cm的若干个小正方体摆成如图所示的立体图形,然后在露出的表面上涂上颜色(不含底面).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com