Question

9．如图①所示，直线L：y=mx+5m与x轴负半轴、y轴正半轴分别交于A、B两点．

（1）当OA=OB时，请确定直线L的解析式．
（2）在（1）的条件下，如图②所示，设Q为AB延长线上一点，作直线OQ，过点A、B两点分别作AM⊥OQ于点M，BN⊥OQ于点N，若AM=4，BN=3，求MN的长．
（3）如图③，当m取不同的值时，点B在y轴正半轴上运动，分别以OB、AB为边，点B为直角顶点，在第一、二象限内作等腰直角三角形OBF和等腰直角三角形ABE，联结EF交y轴于点P，．
问：当点B在y轴正半轴上运动时，试猜想PB的长是否为定值，若是，请求出其值；若不是，请说明理由．

Answer 1

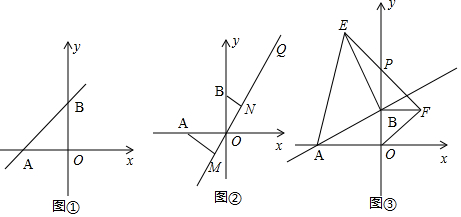
分析 （1）令y=0可求得x=-5，从而可求得点A的坐标，令x=0得y=5m，由OA=OB可知点B的纵坐标为5，从而可求得m的值；
（2）依据AAS证明△AMO≌△ONB，由全等三角形的性质可知ON=AM，OM=BN，最后由MN=AM+BN可求得MN的长；
（3）过点E作EG⊥y轴于G点，先证明△ABO≌△EGB，从而得到BG=10，然后证明△BFP≌△GEP，从而得到BP=GP=$\frac{1}{2}$BG．

解答 解：（1）由题意知：A（-5，0），B（0，5m）
∵OA=OB，
∴5m=5，即m=1．
∴L的解析式y=x+5．

（2）如图②中，

∵AM⊥OQ，BN⊥OQ
∴∠AMO=∠BNO=90°
∴∠AOM+∠MAO=90°
∵∠AOM+BON=90°
∴∠MAO=∠NOB
在△AMO和△ONB中，
$\left\{\begin{array}{l}{∠AMO=∠BNO}\\{∠MAO=∠NOB}\\{OA=OB}\end{array}\right.$，
∴△AMO≌△ONB．
∴ON=AM，OM=BN．
∵AM=4，BN=3，
∴MN=AM+BN=7．

（3）PB的长为定值．
理由：如图③所示：过点E作EG⊥y轴于G点．

∵△AEB为等腰直角三角形，
∴AB=EB，∠ABO+∠EBG=90°．
∵EG⊥BG，
∴∠GEB+∠EBG=90°．
∴∠ABO=∠GEB．
在△ABO和△EGB中，
$\left\{\begin{array}{l}{∠EGB=∠BOA}\\{∠ABO=∠GEB}\\{AB=EB}\end{array}\right.$，
∴△ABO≌△EGB．
∴BG=AO=10，OB=EG
∵△OBF为等腰直角三角形，
∴OB=BF
∴BF=EG．
在△BFP和△GEP中，
$\left\{\begin{array}{l}{∠EGP=∠FBP}\\{∠EPG=∠FPB}\\{EG=BF}\end{array}\right.$，
∴△BFP≌△GEP．
∴BP=GP=$\frac{1}{2}$BG=$\frac{5}{2}$．
∴PB的长为定值．

点评 本题主要考查的是一次函数的综合应用，全等三角形的性质和判定、等腰直角三角形的性质，熟练掌握全等三角形的判定方法是解题的关键学会添加常用辅助线，属于中考常考题型．