
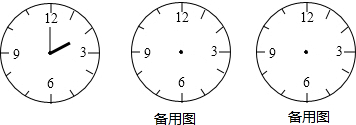
分析 (1)利用钟表表盘的特征解答.表盘共被分成60小格,每一小格所对角的度数为6°.
(2)①可设经过x分钟后,时针与分针第一次成90°角,根据角度差的等量关系列出方程求解即可;
②分三种情况:2时~3时,时针与分针成60°角;3时~4时,时针在前面,分针在后面,时针与分针成60°角;3时~4时,分针在前面,时针在后面,时针与分针成60°角;列出方程求解即可.
解答 解:(1)分针每分针转动了6度,时针每分钟转动了0.5度.
故答案为:6,0.5;
(2)①设经过x分钟后,时针与分针第一次成90°角,依题意有
6x-0.5x-60=90,
解得x=$\frac{300}{11}$.
故经过$\frac{300}{11}$分钟后,时针与分针第一次成90°角;
②2时~3时,时针与分针成60°角,
6m-60-0.5m=60,
解得m=$\frac{240}{11}$;
故3时~4时,时针在前面,分针在后面,时针与分针成60°角,
90+0.5n-6n=60,
解得n=$\frac{60}{11}$;
3时~4时,分针在前面,时针在后面,时针与分针成60°角;
6t-90-0.5t=60,
解得t=$\frac{300}{11}$.
故从2点到4点(不含2点)有3次时针与分针成60°角,分别是2时$\frac{240}{11}$分,3时$\frac{60}{11}$分,3时$\frac{300}{11}$分.
点评 本题考查了钟表问题,解题时经常用到每两个数字之间的度数是30°,分钟每分钟转过的角度为6度,时钟每分钟转过的角度为0.5度.借助图形,更容易解决.同时考查一元一次方程的应用,得到时针所走路程和分针所走路程的等量关系是解决本题的关键.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某商店需要采购甲、乙两种商品共15件,其价格如图所示:且要求乙商品的件数不得少于甲种商品件数的2倍.设购买甲种商品x件,购买两种商品共花费y元.
某商店需要采购甲、乙两种商品共15件,其价格如图所示:且要求乙商品的件数不得少于甲种商品件数的2倍.设购买甲种商品x件,购买两种商品共花费y元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com