
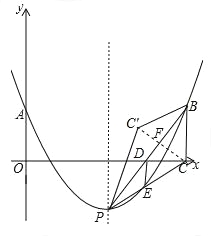
【题目】如图,抛物线y=![]() (其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.
(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.
(1)该抛物线的解析式为 ; (用含m的式子表示);
(2)探究线段DE、BC的关系,并证明你的结论;
(3)直接写出C′点的坐标(用含m的式子表示).

【答案】(1)y=![]() ;(2)DE=
;(2)DE=![]() BC,理由详见解析;(3)(
BC,理由详见解析;(3)(![]() ,
,![]() ).
).
【解析】
试题分析:(1)将点A的坐标代入抛物线解析式,即可求出a的值;
(2)根据抛物线的解析式,求出顶点P的坐标,根据对称轴,求出点B,C的坐标,根据待定系数法求出直线BP、CP的解析式,求出点D、E的坐标,进而求出DE,BC的长度,即可解得;
(3)连接CC′交直线BP于点F,则CC′⊥BP,且CF=C′F,求出CC′的解析式,进而求得点F的坐标,根据CF=C′F,即可解答.
试题解析:(1)把点A(0,m)代入y=![]() ,
,
得:![]() ﹣m=m,
﹣m=m,
am﹣1=0,
∵am>1,
∴a=![]() ,
,
∴y=![]() ,
,
故答案为:y=![]() ;
;
(2)DE=![]() BC.
BC.
理由:又抛物线y=![]() ,可得抛物线的顶点坐标P(
,可得抛物线的顶点坐标P(![]() ,﹣m),
,﹣m),
由l:x=![]() ,可得:点B(
,可得:点B(![]() ,m),
,m),
∴点C(![]() ,0).
,0).
设直线BP的解析式为y=kx+b,点P(![]() ,﹣m)和点B(
,﹣m)和点B(![]() ,m)在这条直线上,
,m)在这条直线上,
得: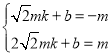 ,解得:
,解得: ,
,
∴直线BP的解析式为:y=![]() ﹣3m,
﹣3m,
令y=0,![]() ﹣3m=0,解得:x=
﹣3m=0,解得:x=![]() ,
,
∴点D(![]() ,0);
,0);
设直线CP的解析式为y=![]() x+
x+![]() ,点P(
,点P(![]() ,﹣m)和点C(
,﹣m)和点C(![]() ,0)在这条直线上,
,0)在这条直线上,
得: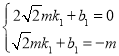 ,解得:
,解得: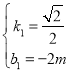 ,
,
∴直线CP的解析式为:y=![]() ﹣2m;
﹣2m;
抛物线与直线CP相交于点E,可得: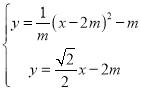 ,解得:
,解得: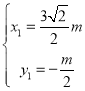 ,
,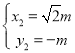 (舍去),
(舍去),
∴点E(![]() ,
,![]() );
);
∵![]() ,
,
∴DE⊥x轴,
∴DE=![]() =
=![]() ,BC=
,BC=![]() =m=2DE,
=m=2DE,
即DE=![]() BC;
BC;
(3)C′(![]() ,
,![]() ).
).
连接CC′,交直线BP于点F,
∵BC′=BC,∠C′BF=∠CBF,
∴CC′⊥BP,CF=C′F,
设直线BP的解析式为y=kx+b,点B(![]() ,m),P(
,m),P(![]() ,﹣m)在直线上,
,﹣m)在直线上,
∴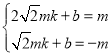 ,解得:
,解得: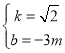 ,
,
∴直线BP的解析式为:y=![]() ﹣3m,
﹣3m,
∵CC′⊥BP,
∴设直线CC′的解析式为:y=![]() ,
,
∴![]() ,解得:
,解得:![]() =2m,
=2m,
联立①②,得: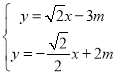 ,解得:
,解得: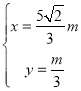 ,
,
∴点F(![]() ,
,![]() ),
),
∴CF=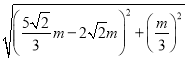 =
=![]() ,
,
设点C′的坐标为(a,![]() ),
),
∴C′F=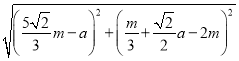 =
=![]() ,解得:a=
,解得:a=![]() ,
,
∴![]() =
=![]() ,
,
∴C′(![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了调查市场上某品牌方便面的色素含量是否符合国家标准,工作人员在超市里随机抽取了某品牌的方便面进行检验.图1和图2是根据调查结果绘制的两幅不完整的统计图,其中A、B、C、D分别代表色素含量为0.05%以下、0.05%~0.1%、0.1%~0.15%、0.15%以上,图1的条形图表示的是抽查的方便面中色素含量分布的袋数,图2的扇形图表示的是抽查的方便面中色素的各种含量占抽查总数的百分比.请解答以下问题: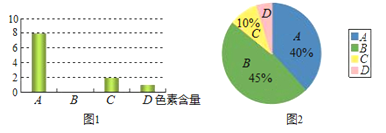
(1)本次调查一共抽查了多少袋方便面?
(2)将图1中色素含量为B的部分补充完整;
(3)图2中的色素含量为D的方便面所占的百分比是多少?
(4)若色素含量超过0.15%即为不合格产品,某超市这种品牌的方便面共有10000袋,那么其中不合格的产品有多少袋?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴交与点E,已知点B(﹣1,0).
(1)点A的坐标: ,点E的坐标: ;
(2)若二次函数y=﹣![]() x2+bx+c过点A、E,求此二次函数的解析式;
x2+bx+c过点A、E,求此二次函数的解析式;
(3)P是线段AC上的一个动点(P与点A、C不重合)连结PB、PD,设L是△PBD的周长,当L取最小值时。
求:①点P的坐标
②判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
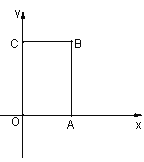
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,OA=4,AB=6,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.
(1)点B的坐标为 ;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光速约为300000千米/秒,用科学记数法表示为( )
A.3×104千米/秒
B.3×105千米/秒
C.3×106千米/秒
D.30×104千米/秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的箱子里共有3个球,把它们的分别编号为1,2,3,这些球除编号不同外其余都相同,从箱子中随机摸出一个球,记录下编号后将它放回箱子,搅匀后再摸出一个球并记录下编号.
(1)用树状图或列表法举出所有可能出现的结果;
(2)求两次摸出的球都是编号为3的球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,2011年经义乌海关出口小商品总价达98.7亿美元据统计,98.7亿美元用科学记数法表示为( )
A.9.87×107美元
B.9.87×108美元
C.9.87×109美元
D.9.87×1010美元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com