
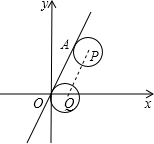
 如图,在平面直角坐标系中,直线l经过原点以及点A(1,$\sqrt{3}$),圆P与直线l相切于点A,若圆P沿直线l滚动一周,点A恰好与原点重合,此时圆心位于点Q,则点Q的坐标为( )
如图,在平面直角坐标系中,直线l经过原点以及点A(1,$\sqrt{3}$),圆P与直线l相切于点A,若圆P沿直线l滚动一周,点A恰好与原点重合,此时圆心位于点Q,则点Q的坐标为( )| A. | ($\frac{1}{2π},-\frac{\sqrt{3}}{π}$) | B. | ($\frac{1}{π},-\frac{\sqrt{3}}{π}$) | C. | ($\frac{\sqrt{3}}{2},-\frac{1}{2}$) | D. | ($\frac{\sqrt{3}}{2π},-\frac{1}{2π}$) |
分析 连接PA、QO,则四边形AOQP是矩形,得出QO=PA,PQ=OA,∠AOQ=90°,由A的坐标得出∠AOx=60°,由勾股定理得出PQ=OA=2,由圆的周长得出2π•OQ=2,求出OQ,作QM⊥x轴于M,由含30°角的直角三角形的性质得出QM=$\frac{1}{2}$OQ=$\frac{1}{2π}$,求出OM=$\sqrt{3}$QM,即可得出结果.
解答 解:连接PA、QO、OQ,如图所示:
则四边形AOQP是矩形,
∴QO=PA,PQ=OA,∠AOQ=90°,
∵A(1,$\sqrt{3}$),
∴∠AOx=60°,PQ=OA=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∵圆P沿直线l滚动一周,点A恰好与原点重合,
∴2π•OQ=2,
解得:OQ=$\frac{1}{π}$,
作QM⊥x轴于M,
∵∠QOM=90°-60°=30°,
∴QM=$\frac{1}{2}$OQ=$\frac{1}{2π}$,
∴OM=$\sqrt{3}$QM=$\frac{\sqrt{3}}{2π}$,
∴Q的坐标为($\frac{\sqrt{3}}{2π}$,-$\frac{1}{2π}$);
故选:D.
点评 本题考查了直线与圆的位置关系、坐标与图形性质、弧长的计算、勾股定理、含30°角的直角三角形的性质等知识;本题有一定难度,由勾股定理求出OQ是解决问题的关键.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
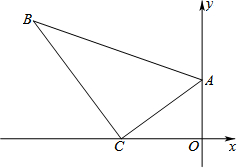 如图,一块直角三角板ABC放置在平面直角坐标系中,∠B=30°,顶点A的坐标为(0,6),直角顶点C的坐标为(-8,0).
如图,一块直角三角板ABC放置在平面直角坐标系中,∠B=30°,顶点A的坐标为(0,6),直角顶点C的坐标为(-8,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
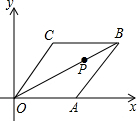 如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4)点P的对角线OB上一个动点,点D的坐标为(0,-2),当DP与AP之和最小时,点P的坐标为($\frac{4}{3}$,$\frac{2}{3}$).
如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4)点P的对角线OB上一个动点,点D的坐标为(0,-2),当DP与AP之和最小时,点P的坐标为($\frac{4}{3}$,$\frac{2}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
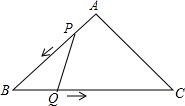 已知:如图,△ABC是等腰直角三角形,∠A=90°,AB=AC=3cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,P的速度是1cm/s,Q的速度是$\sqrt{2}$cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).解答下列问题:
已知:如图,△ABC是等腰直角三角形,∠A=90°,AB=AC=3cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,P的速度是1cm/s,Q的速度是$\sqrt{2}$cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com