
分析 (1)先根据直线y=-3x求出A点的坐标,再把A的坐标代入抛物线的表达式中求出a的值.
(2)把抛物线的解析式化为顶点式,然后再说明需要移动的单位和方向.
解答 解:(1)∵点A(1,m)在直线y=-3x上,
∴m=-3×1=-3.
把x=1,y=-3代入y=ax2+6x-8,求得a=-1.
∴抛物线的解析式是y=-x2+6x-8.
(2)y=-x2+6x-8=-(x-3)2+1.
∴顶点坐标为(3,1).
∴把抛物线y=-x2+6x-8向左平移3个单位长度得到y=-x2+1的图象,再把y=-x2+1的图象向下平移1个单位长度(或向左平移3个单位再向下平移1个单位)得到y=-x2的图象.
点评 本题考查了用待定系数法求函数表达式的方法,同时还考查了抛物线的平移等知识,是比较常见的题目.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
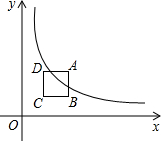 在平面直角坐标系的第一象限内,边长为l的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a).如图,若曲线y=$\frac{4}{x}$(x>0)与此正方形的边有交点,则a的取值范围是2≤a≤3.
在平面直角坐标系的第一象限内,边长为l的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a).如图,若曲线y=$\frac{4}{x}$(x>0)与此正方形的边有交点,则a的取值范围是2≤a≤3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
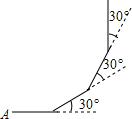 如图:小明从点A出发,沿直线前进5m后向左转30°,再沿直线前进5m后,又向左转30°,照这样方式走下去,他第一次回到出发点A时,一共走了( )
如图:小明从点A出发,沿直线前进5m后向左转30°,再沿直线前进5m后,又向左转30°,照这样方式走下去,他第一次回到出发点A时,一共走了( )| A. | 50m | B. | 60m | C. | 70m | D. | 80m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
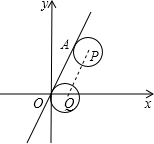 如图,在平面直角坐标系中,直线l经过原点以及点A(1,$\sqrt{3}$),圆P与直线l相切于点A,若圆P沿直线l滚动一周,点A恰好与原点重合,此时圆心位于点Q,则点Q的坐标为( )
如图,在平面直角坐标系中,直线l经过原点以及点A(1,$\sqrt{3}$),圆P与直线l相切于点A,若圆P沿直线l滚动一周,点A恰好与原点重合,此时圆心位于点Q,则点Q的坐标为( )| A. | ($\frac{1}{2π},-\frac{\sqrt{3}}{π}$) | B. | ($\frac{1}{π},-\frac{\sqrt{3}}{π}$) | C. | ($\frac{\sqrt{3}}{2},-\frac{1}{2}$) | D. | ($\frac{\sqrt{3}}{2π},-\frac{1}{2π}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com