
分析 ①根据PA2-PB2=AB2=CD2=PD2-PC2,移项即可;
②过点P作AD的垂线,交AD于点E,交BC于点F,可证四边形ABFE和CDEF为矩形,则AE=BF,DE=CF,在△PAE,△PCF,△PBF,△PCF中,分别求PA2,PC2,PB2,PD2,再比较PA2+PC2与PB2+PD2即可;
③方法同②,根据勾股定理分别求PA2,PC2,PB2,PD2,即可得到结论.
解答 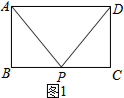 证明:①如图1,P在矩形的边上,
证明:①如图1,P在矩形的边上,
在Rt△ABP中,由勾股定理,得PA2-PB2=AB2,
同理可得PD2-PC2=CD2,
由矩形的性质可得AB=CD,
∴PA2-PB2=PD2-PC2,
∴PA2+PC2=PB2+PD2.
②P在矩形内,如图2,过点P作AD的垂线,交AD于点E,交BC于点F,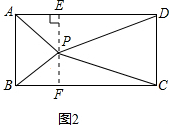
则四边形ABFE和CDEF为矩形,
∴AE=BF,DE=CF,
由勾股定理得:
则AP2=AE2+PE2,PC2=PF2+CF2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AE2+PE2+PF2+CF2,
PB2+PD2=BF2+PF2+DE2+PE2,
∴PA2+PC2=PB2+PD2.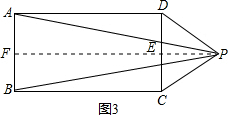
③P在矩形外,如图3,过P作PF⊥AB于F,交CD于E,
则PE⊥CD,
∴四边形AFED与四边形BCEF是矩形,
∴BF=CE,AF=DE,
由勾股定理得:
则AP2=AF2+PF2,PC2=PE2+CE2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AF2+PF2+PE2+CE2,
PB2+PD2=BF2+PF2+DE2+PE2,
∴PA2+PC2=PB2+PD2.
点评 本题考查了勾股定理及矩形的性质.关键是作辅助线,构造直角三角形,利用勾股定理分别表示边长的平方.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
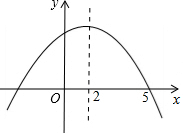 如图,对于二次函数y=ax2+bx+c(a≠0)在x轴上方的图象,当y随x增大而增大时,x的取值范围是( )
如图,对于二次函数y=ax2+bx+c(a≠0)在x轴上方的图象,当y随x增大而增大时,x的取值范围是( )| A. | x<-1 | B. | -1<x<2 | C. | 2<x<5 | D. | x>5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
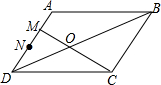 在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )
在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )| A. | $\frac{1}{9}$或$\frac{4}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$或$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
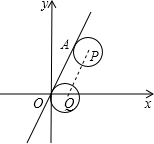 如图,在平面直角坐标系中,直线l经过原点以及点A(1,$\sqrt{3}$),圆P与直线l相切于点A,若圆P沿直线l滚动一周,点A恰好与原点重合,此时圆心位于点Q,则点Q的坐标为( )
如图,在平面直角坐标系中,直线l经过原点以及点A(1,$\sqrt{3}$),圆P与直线l相切于点A,若圆P沿直线l滚动一周,点A恰好与原点重合,此时圆心位于点Q,则点Q的坐标为( )| A. | ($\frac{1}{2π},-\frac{\sqrt{3}}{π}$) | B. | ($\frac{1}{π},-\frac{\sqrt{3}}{π}$) | C. | ($\frac{\sqrt{3}}{2},-\frac{1}{2}$) | D. | ($\frac{\sqrt{3}}{2π},-\frac{1}{2π}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com