
分析 将已知变形进而得出x2-y2=5xy,再整体代入原式求出答案.
解答 解:∵$\frac{y}{x}-\frac{x}{y}$=-5,
∴$\frac{{y}^{2}-{x}^{2}}{xy}$=-5,
∴y2-x2=-5xy,
则x2-y2=5xy
∴$\frac{{3x}^{2}+xy-{3y}^{2}}{{2x}^{2}-xy-{2y}^{2}}$=$\frac{3({x}^{2}-{y}^{2})+xy}{2({x}^{2}-{y}^{2})-xy}$=$\frac{3×5xy+xy}{2×5xy-xy}$=$\frac{16}{9}$.
点评 此题主要考查了分式的化简求值,正确将已知变形是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
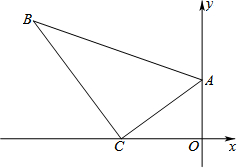 如图,一块直角三角板ABC放置在平面直角坐标系中,∠B=30°,顶点A的坐标为(0,6),直角顶点C的坐标为(-8,0).
如图,一块直角三角板ABC放置在平面直角坐标系中,∠B=30°,顶点A的坐标为(0,6),直角顶点C的坐标为(-8,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售额 | 奖励工资比例 |
| 超过0元但不超过5千元部分 | 5% |
| 超过0.5万元但不超过1万元部分 | 8% |
| 1万元以上的部分 | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $a<\frac{3}{2}$ | B. | $a≤\frac{3}{2}$ | C. | $a>\frac{3}{2}$ | D. | $a≥\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com