
分析 (1)求出根的判别式,利用偶次方的非负性证明;
(2)分△ABC的底边长为2、△ABC的一腰长为2两种情况解答.
解答 (1)证明:△=(k+3)2-4×3k=(k-3)2≥0,
故不论k取何实数,该方程总有实数根;
(2)解:当△ABC的底边长为2时,方程有两个相等的实数根,
则(k-3)2=0,
解得k=3,
方程为x2-6x+9=0,
解得x1=x2=3,
故△ABC的周长为:2+3+3=8;
当△ABC的一腰长为2时,方程有一根为2,
方程为x2-5x+6=0,
解得,x1=2,x2=3,
故△ABC的周长为:2+2+3=7.
点评 本题考查的是一元二次方程根的判别式、等腰三角形的性质,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
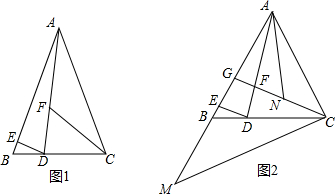
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
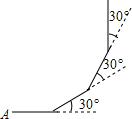 如图:小明从点A出发,沿直线前进5m后向左转30°,再沿直线前进5m后,又向左转30°,照这样方式走下去,他第一次回到出发点A时,一共走了( )
如图:小明从点A出发,沿直线前进5m后向左转30°,再沿直线前进5m后,又向左转30°,照这样方式走下去,他第一次回到出发点A时,一共走了( )| A. | 50m | B. | 60m | C. | 70m | D. | 80m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
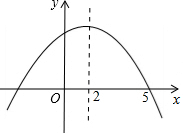 如图,对于二次函数y=ax2+bx+c(a≠0)在x轴上方的图象,当y随x增大而增大时,x的取值范围是( )
如图,对于二次函数y=ax2+bx+c(a≠0)在x轴上方的图象,当y随x增大而增大时,x的取值范围是( )| A. | x<-1 | B. | -1<x<2 | C. | 2<x<5 | D. | x>5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com