
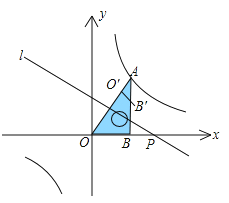
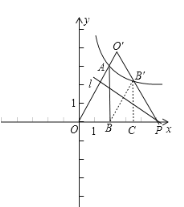
【题目】如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为![]() .在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是OB.
.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是OB.
(1)当点O与点A重合时,点P的坐标是 ;
(2)设P(t,0),当OB与双曲线有交点时,t的取值范围是 .
【答案】(1)(4,0);(2)4≤t≤![]() 或
或![]() ≤t≤-4
≤t≤-4
【解析】
(1)当点O′与点A重合时,即点O与点A重合,进一步解直角三角形AOB,利用轴对称的现在解答即可;
(2)分别求出O′和B′在双曲线上时,P的坐标即可.
解:(1)当点O与点A重合时,
∵∠AOB=60°,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是OB.
AP′=OP′,
∴△AOP′是等边三角形,
∵B(2,0),
∴BO=BP′=2,
∴点P的坐标是(4,0),
(2)∵∠AOB=60°,∠P′MO=90°,
∴∠MP′O=30°,
∴OM=![]() t,OO′=t,
t,OO′=t,
过O′作O′N⊥X轴于N,
∠OO′N=30°,
∴ON=![]() t,NO′=
t,NO′=![]() t,
t,
∴O′(![]() t,
t,![]() t),
t),
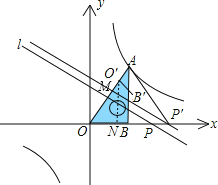
根据对称性可知点P在直线O′B′上,
设直线O′B′的解析式是y=kx+b,代入得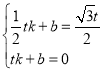 ,
,
解得: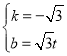 ,
,
∴y=﹣![]() x+
x+![]() t①,
t①,
∵∠ABO=90°,∠AOB=60°,OB=2,
∴OA=4,AB=2![]() ,
,
∴A(2,2![]() )),代入反比例函数的解析式得:k=4
)),代入反比例函数的解析式得:k=4![]() ,
,
∴y=![]() ②,
②,
①②联立得,![]() x2﹣
x2﹣![]() tx+4
tx+4![]() =0,
=0,
即x2﹣tx+4=0③,
b2﹣4ac=t2﹣4×1×4≥0,
解得:t≥4,≤﹣4.
又O′B′=2,根据对称性得B′点横坐标是1+![]() t,
t,
当点B′为直线与双曲线的交点时,
由③得,(x﹣![]() t)2﹣
t)2﹣![]() +4=0,
+4=0,
代入,得(1+![]() t﹣
t﹣![]() t)2﹣
t)2﹣![]() +4=0,
+4=0,
解得t=±2![]() ,
,
而当线段O′B′与双曲线有交点时,
t≤2![]() 或t≥﹣2
或t≥﹣2![]() ,
,
综上所述,t的取值范围是4≤t≤2![]() 或﹣2
或﹣2![]() ≤t≤﹣4.
≤t≤﹣4.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
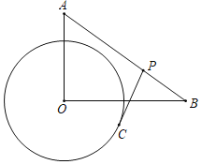
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,⊙O的半径为2,点P是AB边上的动点,过点P作⊙O的一条切线PC(点C为切点),则线段PC长的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AD是△ABC的中线P是线段AD上的一点(不与点A、D重合),连接PB、PC,E、F、G、H分别是AB、AC、PB、PC的中点,AD与EF交于点M;
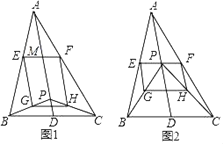
(1)如图1,当AB=AC时,求证:四边形EGHF是矩形;
(2)如图2,当点P与点M重合时,在不添加任何辅助线的条件下,写出所有与△BPE面积相等的三角形(不包括△BPE本身).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若![]() 的长为
的长为![]() π,求“回旋角”∠CPD的度数;
π,求“回旋角”∠CPD的度数;
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
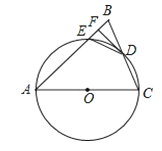
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对函数![]() 的图象和性质进行了探究.已知当自变量
的图象和性质进行了探究.已知当自变量![]() 的值为
的值为![]() 或
或![]() 时,函数值都为
时,函数值都为![]() ;当自变量
;当自变量![]() 的值为
的值为![]() 或
或![]() 时,函数值都为
时,函数值都为![]() .探究过程如下,请补充完整.
.探究过程如下,请补充完整.
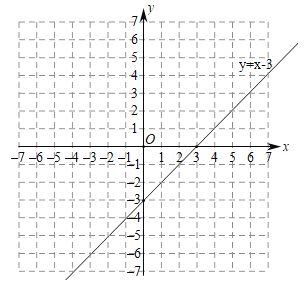
(1)这个函数的表达式为 ;
(2)在给出的平面直角坐标系中,画出这个函数的图象并写出这个函数的--条性质: ;
(3)进一步探究函数图象并解决问题:
①直线![]() 与函数
与函数![]() 有三个交点,则
有三个交点,则![]() ;
;
②已知函数![]() 的图象如图所示,结合你所画的函数图象,写出不等式
的图象如图所示,结合你所画的函数图象,写出不等式![]()
![]() 的解集: .
的解集: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图样中,产生的有害垃圾C所对应的圆心角 度;
(3)调查发现,在可回收物中塑料类垃圾占13%,每回收1吨塑料类垃圾可获得0.5吨二级原料.假设该城市每月产生的生活垃圾为1000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com