
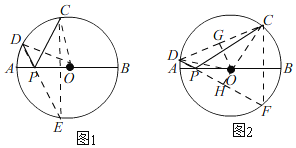
ЁОЬтФПЁПШчЭМЃЌЁбOЕФжБОЖABЃН26ЃЌPЪЧABЩЯ(ВЛгыЕуAЁЂBжиКЯ)ЕФШЮвЛЕуЃЌЕуCЁЂDЮЊЁбOЩЯЕФСНЕуЃЌШєЁЯAPDЃНЁЯBPCЃЌдђГЦЁЯCPDЮЊжБОЖABЕФЁАЛиа§НЧЁБЃЎ
(1)ШєЁЯBPCЃНЁЯDPCЃН60ЁуЃЌдђЁЯCPDЪЧжБОЖABЕФЁАЛиа§НЧЁБТ№ЃПВЂЫЕУїРэгЩЃЛ
(2)Шє![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ІаЃЌЧѓЁАЛиа§НЧЁБЁЯCPDЕФЖШЪ§ЃЛ
ІаЃЌЧѓЁАЛиа§НЧЁБЁЯCPDЕФЖШЪ§ЃЛ
(3)ШєжБОЖABЕФЁАЛиа§НЧЁБЮЊ120ЁуЃЌЧвЁїPCDЕФжмГЄЮЊ24+13![]() ЃЌжБНгаДГіAPЕФГЄЃЎ
ЃЌжБНгаДГіAPЕФГЄЃЎ

ЁОД№АИЁП(1)ЁЯCPDЪЧжБОЖABЕФЁАЛиа§НЧЁБЃЌРэгЩМћНтЮіЃЛ(2)ЁАЛиа§НЧЁБЁЯCPDЕФЖШЪ§ЮЊ45ЁуЃЛ(3)ТњзуЬѕМўЕФAPЕФГЄЮЊ3Лђ23ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЁЯCPDЁЂЁЯBPCЕУЕНЁЯAPDЃЌЕУЕНЁЯBPCЃНЁЯAPDЃЌЫљвдЁЯCPDЪЧжБОЖABЕФЁАЛиа§НЧЁБЃЛЃЈ2ЃЉРћгУCDЛЁГЄЙЋЪНЧѓГіЁЯCODЃН45ЁуЃЌзїCEЁЭABНЛЁбOгкEЃЌСЌНгPEЃЌРћгУЁЯCPDЮЊжБОЖABЕФЁАЛиа§НЧЁБЃЌЕУЕНЁЯAPDЃНЁЯBPCЃЌЁЯOPEЃНЁЯAPDЃЌЕУЕНЁЯOPE+ЁЯCPD+ЁЯBPCЃН180ЁуЃЌМДЕуDЃЌPЃЌEШ§ЕуЙВЯпЃЌЁЯCEDЃН![]() ЁЯCODЃН22.5ЁуЃЌ
ЁЯCODЃН22.5ЁуЃЌ
ЕУЕНЁЯOPEЃН90ЁуЉ22.5ЁуЃН67.5ЁуЃЌдђЁЯAPDЃНЁЯBPCЃН67.5ЁуЃЌЫљвдЁЯCPDЃН45ЁуЃЛЃЈ3ЃЉЗжГіЧщПіPдкOAЩЯЛђепOBЩЯЕФЧщПіЃЌдкOAЩЯЪБЃЌЭЌРэЃЈ2ЃЉЕФЗНЗЈЕУЕНЕуDЃЌPЃЌFдкЭЌвЛЬѕжБЯпЩЯЃЌЕУЕНЁїPCFЪЧЕШБпШ§НЧаЮЃЌСЌНгOCЃЌODЃЌЙ§ЕуOзїOGЁЭCDгкGЃЌ
РћгУsinЁЯDOGЃЌЧѓЕУCDЃЌРћгУжмГЄЧѓЕУDFЃЌЙ§OзїOHЁЭDFгкHЃЌРћгУЙДЙЩЖЈРэЧѓЕУOPЃЌНјЖјЕУЕНAPЃЛдкOBЩЯЪБЃЌЭЌРэOAМЦЫуЗНЗЈМДПЩ
ЁЯCPDЪЧжБОЖABЕФЁАЛиа§НЧЁБЃЌ
РэгЩЃКЁпЁЯCPDЃНЁЯBPCЃН60ЁуЃЌ
ЁрЁЯAPDЃН180ЁуЉЁЯCPDЉЁЯBPCЃН180ЁуЉ60ЁуЉ60ЁуЃН60ЁуЃЌ
ЁрЁЯBPCЃНЁЯAPDЃЌ
ЁрЁЯCPDЪЧжБОЖABЕФЁАЛиа§НЧЁБЃЛ
(2)ШчЭМ1ЃЌЁпABЃН26ЃЌ
ЁрOCЃНODЃНOAЃН13ЃЌ
ЩшЁЯCODЃНnЁуЃЌ
Ёп![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ІаЃЌ
ІаЃЌ
Ёр![]()
ЁрnЃН45ЃЌ
ЁрЁЯCODЃН45ЁуЃЌ
зїCEЁЭABНЛЁбOгкEЃЌСЌНгPEЃЌ
ЁрЁЯBPCЃНЁЯOPEЃЌ
ЁпЁЯCPDЮЊжБОЖABЕФЁАЛиа§НЧЁБЃЌ
ЁрЁЯAPDЃНЁЯBPCЃЌ
ЁрЁЯOPEЃНЁЯAPDЃЌ
ЁпЁЯAPD+ЁЯCPD+ЁЯBPCЃН180ЁуЃЌ
ЁрЁЯOPE+ЁЯCPD+ЁЯBPCЃН180ЁуЃЌ
ЁрЕуDЃЌPЃЌEШ§ЕуЙВЯпЃЌ
ЁрЁЯCEDЃН![]() ЁЯCODЃН22.5ЁуЃЌ
ЁЯCODЃН22.5ЁуЃЌ
ЁрЁЯOPEЃН90ЁуЉ22.5ЁуЃН67.5ЁуЃЌ
ЁрЁЯAPDЃНЁЯBPCЃН67.5ЁуЃЌ
ЁрЁЯCPDЃН45ЁуЃЌ
МДЃКЁАЛиа§НЧЁБЁЯCPDЕФЖШЪ§ЮЊ45ЁуЃЌ
(3)ЂйЕБЕуPдкАыОЖOAЩЯЪБЃЌШчЭМ2ЃЌЙ§ЕуCзїCFЁЭABНЛЁбOгкFЃЌСЌНгPFЃЌ
ЁрPFЃНPCЃЌ
ЭЌ(2)ЕФЗНЗЈЕУЃЌЕуDЃЌPЃЌFдкЭЌвЛЬѕжБЯпЩЯЃЌ
ЁпжБОЖABЕФЁАЛиа§НЧЁБЮЊ120ЁуЃЌ
ЁрЁЯAPDЃНЁЯBPCЃН30ЁуЃЌ
ЁрЁЯCPFЃН60ЁуЃЌ
ЁрЁїPCFЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯCFDЃН60ЁуЃЌ
СЌНгOCЃЌODЃЌ
ЁрЁЯCODЃН120ЁуЃЌ
Й§ЕуOзїOGЁЭCDгкGЃЌ
ЁрCDЃН2DGЃЌЁЯDOGЃН![]() ЁЯCODЃН60ЁуЃЌ
ЁЯCODЃН60ЁуЃЌ
ЁрDGЃНODsinЁЯDOGЃН13ЁСsin60ЁуЃН![]()
ЁрCDЃН![]() ЃЌ
ЃЌ
ЁпЁїPCDЕФжмГЄЮЊ24+13![]() ЃЌ
ЃЌ
ЁрPD+PCЃН24ЃЌ
ЁпPCЃНPFЃЌ
ЁрPD+PFЃНDFЃН24ЃЌ
Й§OзїOHЁЭDFгкHЃЌ
ЁрDHЃН![]() DFЃН12ЃЌ
DFЃН12ЃЌ
дкRtЁїOHDжаЃЌOHЃН![]()
дкRtЁїOHPжаЃЌЁЯOPHЃН30ЁуЃЌ
ЁрOPЃН10ЃЌ
ЁрAPЃНOAЉOPЃН3ЃЛ
ЂкЕБЕуPдкАыОЖOBЩЯЪБЃЌ
ЭЌЂйЕФЗНЗЈЕУЃЌBPЃН3ЃЌ
ЁрAPЃНABЉBPЃН23ЃЌ
МДЃКТњзуЬѕМўЕФAPЕФГЄЮЊ3Лђ23ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЦпФъМЖ10ИіАрЕФ300УћбЇЩњМДНЋВЮМгбЇаЃОйааЕФбаОПТУааЛюЖЏЃЌбЇаЃЬсГівдЯТ4ИіЛюЖЏжїЬтЃКAЃЎГрЫЎЕЄЯМЕиУВПМВьЃЛBЃЎЦНЬСЬьЮФжЊЪЖПМВьЃЛCЃЎЩНЙиКьЩЋЮФЛЏПМВьЃЛDЃЎКЃСњЕчЭСЫОЮФЛЏПМВьЃЌЮЊСЫНтбЇЩњЯВЛЖЕФЛюЖЏжїЬтЃЌбЇЩњЛсПЊеЙСЫвЛДЮЕїВщбаОПЃЌЧыНЋЯТУцЕФЙ§ГЬВЙШЋ
ЃЈ1ЃЉЪеМЏЪ§ОнЃКбЇЩњЛсМЦЛЎЕїВщбЇЩњЯВЛЖЕФЛюЖЏжїЬтЧщПіЃЌЯТУцГщбљЕїВщЕФЖдЯѓбЁдёКЯРэЕФЪЧ______ЃЎЃЈЬюађКХЃЉ
ЂйбЁдёЦпФъМЖ3АрЁЂ4АрЁЂ5АрбЇЩњзїЮЊЕїВщЖдЯѓ
ЂкбЁдёбЇаЃТУгЮЩугАЩчЭХЕФбЇЩњзїЮЊЕїВщЖдЯѓ
ЂлбЁдёИїАрбЇКХЮЊ6ЕФБЖЪ§ЕФбЇЩњзїЮЊЕїВщЖдЯѓ
ЃЈ2ЃЉећРэЁЂУшЪіЪ§ОнЃКЭЈЙ§ЕїЫКѓЃЌбЇЩњЛсЭЌбЇЛцжЦСЫШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыАбЭГМЦЭМВЙГфЭъећ
ФГаЃЦпФъМЖбЇЩњЯВЛЖЕФЛюЖЏжїЬтЬѕаЮЭГМЦЭМФГаЃЦпФъМЖбЇЩњЯВЛЖЕФЛюЖЏжїЬтЩШаЮЭГМЦЭМ
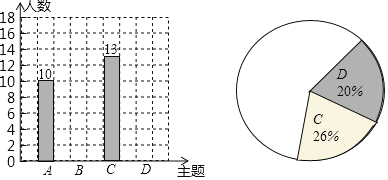
ЃЈ3ЃЉЗжЮіЪ§ОнЁЂЭЦЖЯНсТлЃКЧыФуИљОнЩЯЪіЕїВщНсЙћЯђбЇаЃЭЦМіБОДЮЛюЖЏЕФжїЬтЃЌФуЕФЭЦМіЪЧ______ЃЈЬюA-DЕФзжФИДњКХЃЉЃЌЙРЫуШЋФъМЖДѓдМгаЖрЩйУћбЇЩњЯВЛЖетИіжїЬтЛюЖЏ
ЃЈ4ЃЉШєдк5УћбЇЩњЛсИЩВПЃЈ3Фа2ХЎЃЉжаЃЌЫцЛњбЁШЁ2УћЭЌбЇЕЃШЮЛюЖЏЕФзщГЄКЭИБзщГЄЃЌЧѓГщГіЕФСНУћЭЌбЇЧЁКУЪЧ1Фа1ХЎЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ФкНггкдВ
ФкНггкдВ![]() ЃЌЕу
ЃЌЕу![]() ЮЊЛЁ
ЮЊЛЁ![]() ЩЯвЛЕуЃЌСЌНг
ЩЯвЛЕуЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
 ЁЁЁЁЁЁЁЁЁЁ
ЁЁЁЁЁЁЁЁЁЁ ЁЁЁЁЁЁЁЁЁЁ
ЁЁЁЁЁЁЁЁЁЁ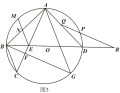
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКЛЁ![]() ЛЁ
ЛЁ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌНЛдВ
ЃЌНЛдВ![]() Еу
Еу![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌдВ![]() ЩЯвЛЕу
ЩЯвЛЕу![]() гыЕу
гыЕу![]() Йигк
Йигк![]() ЖдГЦЃЌСЌНг
ЖдГЦЃЌСЌНг![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊЛЁ
ЮЊЛЁ![]() ЩЯвЛЕуЃЌ
ЩЯвЛЕуЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФжмГЄЮЊ20ЃЌ
ЕФжмГЄЮЊ20ЃЌ![]() ЃЌЧѓдВ
ЃЌЧѓдВ![]() АыОЖЃЎ
АыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
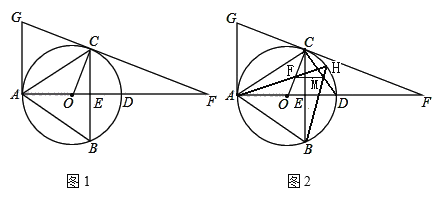
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCФкНггкЁбOЃЌжБОЖADНЛBCгкЕуEЃЌбгГЄADжСЕуFЃЌЪЙDFЃН2ODЃЌСЌНгFCВЂбгГЄНЛЙ§ЕуAЕФЧаЯпгкЕуGЃЌЧвТњзуAGЁЮBCЃЌСЌНгOCЃЌШєcosЁЯBACЃН![]() ЃЌBCЃН8ЃЎ
ЃЌBCЃН8ЃЎ
ЃЈ1ЃЉЧѓжЄЃКCFЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЧѓЁбOЕФАыОЖOCЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЁбOЕФЯвAHОЙ§АыОЖOCЕФжаЕуFЃЌСЌНсBHНЛЯвCDгкЕуMЃЌСЌНсFMЃЌЪдЧѓГіFMЕФГЄКЭЁїAOFЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
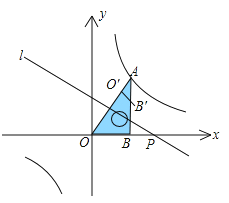
ЁОЬтФПЁПШчЭМЃЌНЋвЛПщжБНЧШ§НЧАхOABЗХдкЦНУцжБНЧзјБъЯЕжаЃЌB(2ЃЌ0)ЃЌЁЯAOB=60ЁуЃЌЕуAдкЕквЛЯѓЯоЃЌЙ§ЕуAЕФЫЋЧњЯпЮЊ![]() .дкxжсЩЯШЁвЛЕуPЃЌЙ§ЕуPзїжБЯпOAЕФДЙЯпlЃЌвджБЯпlЮЊЖдГЦжсЃЌЯпЖЮOBОжсЖдГЦБфЛЛКѓЕФЯёЪЧOBЃЎ
.дкxжсЩЯШЁвЛЕуPЃЌЙ§ЕуPзїжБЯпOAЕФДЙЯпlЃЌвджБЯпlЮЊЖдГЦжсЃЌЯпЖЮOBОжсЖдГЦБфЛЛКѓЕФЯёЪЧOBЃЎ
ЃЈ1ЃЉЕБЕуOгыЕуAжиКЯЪБЃЌЕуPЕФзјБъЪЧ ЃЛ
ЃЈ2ЃЉЩшP(tЃЌ0)ЃЌЕБOBгыЫЋЧњЯпгаНЛЕуЪБЃЌtЕФШЁжЕЗЖЮЇЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЫЎЙћЯњЪлЭњМОЃЌФГЫЎЙћЕъЙКНјвЛгХжЪЫЎЙћЃЌНјМлЮЊ20дЊ/ЧЇПЫЃЌЪлМлВЛЕЭгк20дЊ/ЧЇПЫЃЌЧвВЛГЌЙ§32дЊ/ЧЇПЫЃЌИљОнЯњЪлЧщПіЃЌЗЂЯжИУЫЎЙћвЛЬьЕФЯњЪлСПyЃЈЧЇПЫЃЉгыИУЬьЕФЪлМлxЃЈдЊ/ЧЇПЫЃЉТњзуШчЯТБэЫљЪОЕФвЛДЮКЏЪ§ЙиЯЕЃЎ
ЯњЪлСПyЃЈЧЇПЫЃЉ | Ё | 34.8 | 32 | 29.6 | 28 | Ё |
ЪлМлxЃЈдЊ/ЧЇПЫЃЉ | Ё | 22.6 | 24 | 25.2 | 26 | Ё |
ЃЈ1ЃЉФГЬьетжжЫЎЙћЕФЪлМлЮЊ23.5дЊ/ЧЇПЫЃЌЧѓЕБЬьИУЫЎЙћЕФЯњЪлСПЃЎ
ЃЈ2ЃЉШчЙћФГЬьЯњЪлетжжЫЎЙћЛёРћ150дЊЃЌФЧУДИУЬьЫЎЙћЕФЪлМлЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЙигкxЕФВЛЕШЪНзщ![]() ЮоНтЃЌЧвЙигкyЕФЗжЪНЗНГЬ
ЮоНтЃЌЧвЙигкyЕФЗжЪНЗНГЬ![]() гаЗЧе§ећЪ§НтЃЌдђЗћКЯЬѕМўЕФЫљгаећЪ§kЕФжЕжЎКЭЮЊЃЈЁЁЁЁЃЉ
гаЗЧе§ећЪ§НтЃЌдђЗћКЯЬѕМўЕФЫљгаећЪ§kЕФжЕжЎКЭЮЊЃЈЁЁЁЁЃЉ
A.Љ7B.Љ12C.Љ20D.Љ34
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
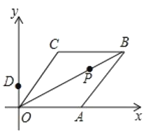
ЁОЬтФПЁПШчЭМЃЌвбжЊСтаЮ![]() ЕФБп
ЕФБп![]() дк
дк![]() жсЩЯЃЌЕу
жсЩЯЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЪЧЖдНЧЯп
ЪЧЖдНЧЯп![]() ЩЯЕФвЛИіЖЏЕуЃЌЕу
ЩЯЕФвЛИіЖЏЕуЃЌЕу![]() дк
дк![]() жсЩЯЃЌЕБ
жсЩЯЃЌЕБ![]() зюЖЬЪБЃЌЕу
зюЖЬЪБЃЌЕу![]() ЕФзјБъЮЊ______.
ЕФзјБъЮЊ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌОиаЮABCDЕФвЛБпBCдкжБНЧзјБъЯЕжаxжсЩЯЃЌелЕўБпADЃЌЪЙЕуDТфдкxжсЩЯЕуFДІЃЌелКлЮЊAEЃЌвбжЊABЃН8ЃЌADЃН10ЃЌВЂЩшЕуBзјБъЮЊЃЈmЃЌ0ЃЉЃЌЦфжаmЃМ0ЃЎ
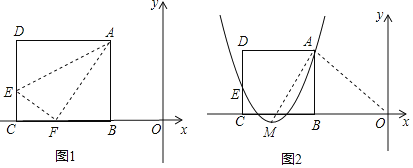
ЃЈ1ЃЉЧѓЕуEЁЂFЕФзјБъЃЈгУКЌmЕФЪНзгБэЪОЃЉЃЛ
ЃЈ2ЃЉСЌНгOAЃЌШєЁїOAFЪЧЕШбќШ§НЧаЮЃЌЧѓmЕФжЕЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЩшХзЮяЯпyЃНaЃЈxЉm+6ЃЉ2+hОЙ§AЁЂEСНЕуЃЌЦфЖЅЕуЮЊMЃЌСЌНгAMЃЌШєЁЯOAMЃН90ЁуЃЌЧѓaЁЂhЁЂmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com